Next: A. 体問題全体像 Up: 3 一般の場合の解析 Previous: 3.1 Kepler の第二法則 (面積測度一定の法則)
以下、Kepler の第一法則を証明する。
すなわち軌道が楕円であることを証明するが、
得られるのは、
![]() の軌跡であって、
の軌跡であって、
![]() そのものではない。
細かい注意になるが、これは微分方程式を解いたのとは少し異なる。
そのものではない。
細かい注意になるが、これは微分方程式を解いたのとは少し異なる。
軌道の解析に戻る。
![]() を従属変数、
を従属変数、![]() を独立変数と考えることになる。
を独立変数と考えることになる。
![]() を
を ![]() に関する微分を表わす記号とする。
に関する微分を表わす記号とする。
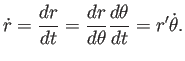
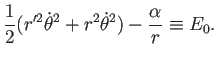
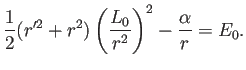
![$\displaystyle \frac{k^2}{2}
\left[
\left(\frac{r'}{r^2}\right)^2+\frac{1}{r^2}
\right]
-\frac{\alpha}{r}=E_0.
$](img96.png)
![]() とおくと、
とおくと、
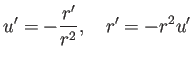
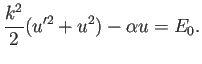
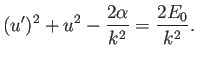
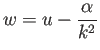
![]() の場合を考えると
の場合を考えると ![]() は定数。
は定数。![]() も定数。
も定数。
![]() も定数。これは円軌道の場合であり、前節で解析済みである
(等速円運動になる)。
も定数。これは円軌道の場合であり、前節で解析済みである
(等速円運動になる)。
![]() の場合。一般解は
の場合。一般解は
(4) に代入すると
![]() となるので、
となるので、
![]() .
.
極座標の原線を ![]() が最小になる点を通るように取れば
が最小になる点を通るように取れば ![]() となる
(必ず最小になるのか?単に座標系を取り直すことでくらいにしておく方がよいな)。
となる
(必ず最小になるのか?単に座標系を取り直すことでくらいにしておく方がよいな)。
![]() 次曲線の極座標表示の標準形と見比べよう。
次曲線の極座標表示の標準形と見比べよう。
桂田 祐史