G. 専用の関数を使ってみる -- Python, Julia

常微分方程式を数値的に解くためのコードは、 Runge-Kutta 法でよければ、自作するのはそれほど難しくない、 それを実行してみよう、 ということで、 以前書いた文書のリニューアルの意味を込めてこの文書を書いたわけだが、 そもそも 2021年にもなってまだその方針でやっているのが間違っている、 という気もする。

今では、Mathematica, MATLAB, Python, Julia, … などなど、 専用の関数が用意されている処理系は簡単に利用可能である。

(以前でも、固有値問題などは専門家の作ったライブラリィを利用していたし。 常微分方程式を解く手段も、そういうのに切り替えるべきなのかもしれない。)

ここでは、そういうやり方を紹介してみる。

例題として、無次元化した SIR モデル

$$\frac{\D S}{\D t}=-R_0 S I,$$

$$\frac{\D I}{\D t}=R_0 S I-I,$$

$$\frac{\D R}{\D t}=I$$

を取り上げる。ここで $R_0$ は基本再生算数と呼ばれる正の定数である。

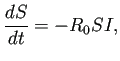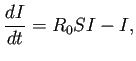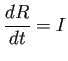参考「SIRモデルについてのメモ」
http://nalab.mind.meiji.ac.jp/~mk/labo/text/sir.pdf
特に§3「方程式の無次元化と解の性質」の§3.2

初期条件として

$$S(0)=1-I_0,\quad I(0)=I_0,\quad R(0)=0.$$ (44)

ここで $I_0$ は $0<I_0\ll 1$ を満たす数とする。 ある感染症について、 免疫を持たない集団に少数の感染者が侵入してどうなるか、という話。