- ...)1
- T. R. Malthus (1766–-1834)
は英国の経済学者で、1798年に『人口の原理』を著わし、
人口は幾何級数的 (≒等比数列的=指数関数的 )に増加しうるが、
生存手段は算術級数的 (=等差数列的= 1次関数的) にしか増加しないと論じた。
これを書いている2021年は COVID19 が流行している。
感染者は指数関数的に増加するが、病床は…、
だから感染を抑えることが重要である、
ということを理解できない人が少なくない。
そういえばウィキペディアのマルサスの項目を見ても、
マルサスが何度も書いて強調していることが載っていない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を求めることを目標とする2
- つまり、
変数
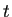 の離散的な値に対する解の値のみを求める、
という意味で「離散変数法」なわけである。
このように目標を低く設定することによって、
無限次元の問題が有限次元の問題に簡略化されていると言える。
の離散的な値に対する解の値のみを求める、
という意味で「離散変数法」なわけである。
このように目標を低く設定することによって、
無限次元の問題が有限次元の問題に簡略化されていると言える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 法である3
- 後退Euler法
というものがあるので、それと区別するために前進Euler法とも呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 法という4
- Runge-Kutta法にはたくさんの親戚がいるので、
ここで紹介したものを、
「古典的Runge-Kutta法」、「4次のRunge-Kutta法」と呼ぶこともある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
次のどちらかになるだろうか?5
- もっと効率的に出来なくはないけれど、
ここでは分かりやすさ優先のコードにした。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を計算して6
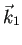 ,
, 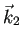 ,
, 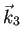 ,
, 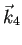 は
は 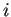 に
依存するので、
本来は
に
依存するので、
本来は
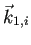 のように
のように 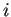 を含める記号を用いるべきだがサボっている。
を含める記号を用いるべきだがサボっている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.