Next: 3.3 C言語によるプログラム例 Up: 3 2次元の問題 Previous: 3.1 ターゲット問題 van der
Euler法の場合は
| (14) |
そうでない場合もこの式を成分表示した
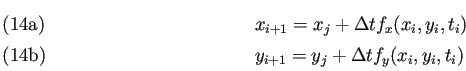 |
実際には、![]() ,
, ![]() は配列 x[], y[] ではなく、
スカラー変数 x, y に記憶することが多いであろうから、
次のどちらかになるだろうか?5
は配列 x[], y[] ではなく、
スカラー変数 x, y に記憶することが多いであろうから、
次のどちらかになるだろうか?5
dx = dt * fx(x,y,t); dy = dt * fy(x,y,t); x += dx; y += dy; |
newx = x + dt * fx(x,y,t); newy = y + dt * fy(x,y,t); x = newx; y = newy; |
Runge-Kutta法の場合は
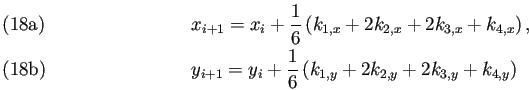 |
この例では ![]() が
が![]() 次元であるから、
(18a)-(18h) という8つの式で済んでいるが、
ベクトル
次元であるから、
(18a)-(18h) という8つの式で済んでいるが、
ベクトル ![]() の次元
の次元 ![]() が高くなると面倒になる。
その場合は、
が高くなると面倒になる。
その場合は、
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() などを配列で取り扱うプログラムが多い
(この文書ではそれは説明しない)。
などを配列で取り扱うプログラムが多い
(この文書ではそれは説明しない)。
桂田 祐史