2.8 プログラムの書き方

$$A=L U$$   $$\mbox{($L$ は下三角行列, $U$ は上三角行列)}$$

と LU 分解できるとき、 $L$ と $U$ を計算機で計算することを考える。

二つの行列 $L$ と $U$ を記憶するには、 行列ちょうど $1$ 個分の $n^2$ 個の成分を記憶できれば十分である。 つまり

$$L=(\ell_{ij}),\quad U=(u_{ij})$$

とするとき、

$$i=j\quad\Then\quad \ell_{ij}=1,\qquad i<j\quad\Then\quad \ell_{ij}=0,\qquad i>j\quad\Then\quad u_{ij}=0$$

が分かっているので、 それらについては記憶しておく必要がない。

上の例で

$$A= \left( \begin{array}{cccc} 2&3&-1 \\ 4&4&-3 \\ -2&3&-1 \end{array}\right)$$

から

$$L= \left( \begin{array}{rrr} 1 & 0 & 0 \\ \mbox{\textcolor{red}{... ...olor{blue}{$-1$}} \\ 0 & 0 & \mbox{\textcolor{blue}{$-5$}} \end{array}\right)$$

を得たいわけだが、$L$ の対角線より上 (含む対角線) と、 $U$ の対角線から下 (対角線は含まない) は不要なので、 結果を

$$\left( \begin{array}{rrr} \mbox{\textcolor{blue}{$2$}} & \mbox{... ...ox{\textcolor{red}{$-3$}} & \mbox{\textcolor{blue}{$-5$}} \end{array} \right)$$

という形に圧縮することができる。

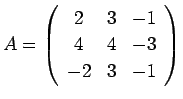
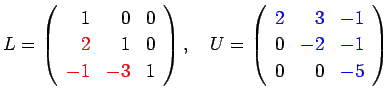
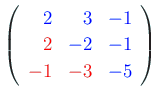
そこで実際のプログラムでは、 次のようなコーディングをする。

C 言語風疑似プログラム

  for (k = 1; k < n; k++) {
    /* (k,k) 成分で掃き出す */
    for (i = k + 1; k <= n; k++) {
      /* q_{ik} = a_{ik} / a_{kk} を求める */
      q = a[i][k] / a[k][k];
      /* i 行から第 k 行の q 倍を引く (ただし計算は j (≧k+1) 列のみ実行) */
      for (j = k + 1; j <= n; j++)
        a[i][j] -= q * a[k][j];
      /* q_{ik} = L_{ik} を記憶しておく (記憶不要になったメモリーを利用) */
      a[i][k] = q;
    }
  }

この事情は、係数行列が疎行列の場合も基本的には変らない。 例えば三重対角行列を LU 分解し、 それを用いて連立1次方程式を解く プログラムを末尾に引用するが、 LU 分解の部分は

三重対角行列のLU分解

/* 前進消去 (forward elimination) */
for (k = 1; k < n; k++) {
  al[k + 1] /= ad[k];             /* a[i][k] /= a[k][k] */
  ad[k + 1] -= au[k] * al[k + 1]; /* a[i][j] -= a[k][j] * q  (jはk+1のみ) */
}

と非常にコンパクトに記述できている ($A$ が三重対角行列の場合は、 上三角因子 $U$ の対角線より上の部分はもとの行列 $A$ のそれと同じ (なぜそうなるか考えて確かめよ) という特徴があるため、 j に関するループが一つの代入文に置き換わっている。 また下三角因子 $L$ は、 対角線と、対角線より1つ下のところにだけ非零成分が存在しうる。 こういう事情のおかげで、プログラムは極限までコンパクトになっている)。

以下、三重対角行列 $A$ の LU 分解が得られているとして、 連立1次方程式 $A x=b$ をどうやって解くか述べる。 すでに説明したように、$Ly = b$, $A x=y$ という二つの方程式に分解する。 $Ly = b$ を解く部分は、 $\ell_{ii}=1$ と、三重対角であることに注意すると

$$y_1=b_1,$$

そして $i=2,3,\dots,n$ の順に

$$y_i=b_i-\ell_{i,i-1}y_{i-1}$$

とすればよい。最初に b[] に $b$ が記憶されていれば

  for (i = 2; i <= n; i++)
    b[i] -= al[i] * b[i-1];

というコードで計算すると b[] に $y$ が計算 (して記憶) される。

次に $A x=y$ を解く部分は

$$x_n=\frac{y_n}{u_{nn}}$$

としてから、 $i=n-1,n-2,\dots,1$ の順に

$$x_i=\frac{(y_i-u_{i,i+1}x_{i+1})}{u_{ii}}$$

とすればよい。b[] に $y$ が記憶されていれば

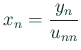
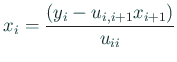
  b[n] /= ad[n];
  for (i = n-1; i >= 1; i--)
    b[i] = (b[i] - au[i] * b[i+1]) / ad[i];

というコードで計算すると b[] に $x$ が記憶 (して記憶) される。