3重対角行列のLU分解プログラム

/* trid-lu1.c -- 3項方程式を Gauss の消去法で解く */

#include "trid-lu1.h"

/* 3項方程式 (係数行列が三重対角である連立1次方程式のこと) Ax=b を解く
 *
 *   入力
 *     n: 未知数の個数
 *     al,ad,au: 連立1次方程式の係数行列
 *       (al: 対角線の下側 i.e. 下三角部分 (lower part)
 *        ad: 対角線       i.e. 対角部分 (diagonal part)
 *        au: 対角線の上側 i.e. 上三角部分 (upper part)
 *        つまり
 *
 *         ad[1] au[1]   0   .................. 0
 *         al[2] ad[2] au[2]   0  ............. 0
 *           0   al[3] ad[3] au[3]  0 ......... 0
 *                         ....................
 *                         al[n-1] ad[n-1] au[n-1]
 *                           0     al[n]   ad[n]

 *        al[i] = A_{i,i-1}, ad[i] = A_{i,i}, au[i] = A_{i,i+1},
 *        al[1], au[n] は意味がない)
 *
 *     b: 連立1次方程式の右辺の既知ベクトル
 *        (添字は 1 から。i.e. b[1],b[2],...,b[n] にデータが入っている。)
 *   出力
 *     al,ad,au: 入力した係数行列を LU 分解したもの
 *     b: 連立1次方程式の解
 *   能書き
 *     一度 call すると係数行列を LU 分解したものが返されるので、
 *     以後は同じ係数行列に関する連立1次方程式を解くために、
 *     関数 trisol1() が使える。
 *   注意
 *     Gauss の消去法を用いているが、ピボットの選択等はしていな
 *     いので、ピボットの選択をしていないので、係数行列が正定値である
 *     などの適切な条件がない場合は結果が保証できない。
 */

void trid1(int n, double *al, double *ad, double *au, double *b)
{
  trilu1(n,al,ad,au);
  trisol1(n,al,ad,au,b);
}

/* 三重対角行列の LU 分解 (pivoting なし) */
void trilu1(int n, double *al, double *ad, double *au)
{
  int i;
  /* 前進消去 (forward elimination) */
  for (i = 1; i < n; i++) {
    al[i + 1] /= ad[i];
    ad[i + 1] -= au[i] * al[i + 1];
  }
}

/* LU 分解済みの三重対角行列を係数に持つ3項方程式を解く */
void trisol1(int n, double *al, double *ad, double *au, double *b)
{
  int i;
  /* 前進消去 (forward elimination) */
  for (i = 1; i < n; i++) b[i + 1] -= b[i] * al[i + 1];
  /* 後退代入 (backward substitution) */
  b[n] /= ad[n];
  for (i = n - 1; i >= 1; i--) b[i] = (b[i] - au[i] * b[i + 1]) / ad[i];
}

これを使って、

$$A= \left( \begin{array}{rrr} 2 & 3 & 0 \\ 4 & 4 & -3 \\ 0 & 3 & -1 \end{array} \right)$$

が

$$A=L U,\quad L=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 1 &... ...} 2 & 3 & 0 \\ 0 & -2 & -3 \\ 0 & 0 & -\frac{11}{2} \end{array} \right),$$

と LU 分解されることを確かめてみよう。

/*
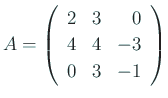
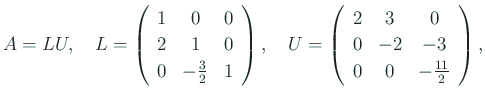
 * test-trid-lu1.c
 *   gcc -o test-trid-lu1 test-trid-lu1.c trid-lu1.c
 */

#include <stdio.h>
#include "trid-lu1.h"

#define N 3

int main(void)
{
  int n;
  double al[N+1], ad[N+1], au[N+1], b[N+1];
  n = 3;
  /* 行列 A の設定 */
  ad[1] = 2; au[1] = 3;
  al[2] = 4; ad[2] = 4; au[2] = -3;
             al[3] = 3; ad[3] = -1;
  /* A の LU 分解 */
  trilu1(n, al, ad, au);
  /* LU 分解の結果の表示 */
  printf("%f %f %f\n", ad[1], au[1], 0.0);
  printf("%f %f %f\n", al[2], ad[2], au[2]);
  printf("%f %f %f\n", 0.0,   al[3], ad[3]);
  /* x=(1,2,3) に対応する b=A x */
  b[1] = 8; b[2] = 3; b[3] = 3;
  /* A x = b を解く */
  trisol1(n, al, ad, au, b);
  /* 解を表示する */
  printf("%f %f %f\n", b[1], b[2], b[3]);

  return 0;
}

oyabun% gcc -o test-trid-lu1 test-trid-lu1.c trid-lu1.c
oyabun% ./test-trid-lu1
2.000000 3.000000 0.000000
2.000000 -2.000000 -3.000000
0.000000 -1.500000 -5.500000
1.000000 2.000000 3.000000
oyabun%