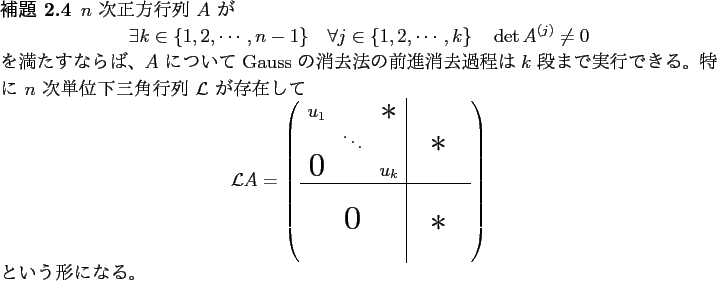
以下、行列 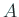 に対して、
に対して、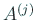 で、
で、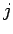 次の主座小行列を表す:
次の主座小行列を表す:
蛇足ながら、数値計算言語の MATLAB では、
a という行列に対して、
a(1:j,1:j) という式で 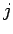 次の主座小行列を表せる。
次の主座小行列を表せる。
証明.
行列を
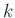
行,
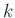
列のところで線を引いてブロックわけする:
(
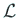
の右上のブロック、
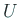
の左下のブロックは零行列ということを主張している。)
であるから、
正則
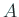
が LU 分解
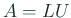
を持つとする。
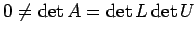
より、
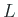
と
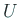
も正則である。
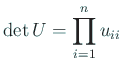
より、
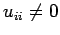
(
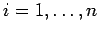
).
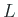
の逆行列を
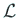
とすると、
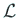
は下三角で、
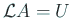
が成り立つから、前半を用いて、
これから
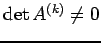
.


逆に
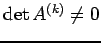 (
(
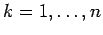 ) ならば
) ならば 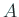 は LU 分解できる
ことを示すには、Gauss の消去法によって具体的に LU 分解を構成してみせる。
は LU 分解できる
ことを示すには、Gauss の消去法によって具体的に LU 分解を構成してみせる。
証明.
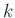
についての帰納法による。
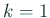
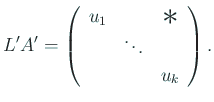
のとき、
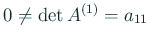
より、
第 1 列の対角線より下を掃き出すことができる。実際
とおくと、
ゆえに
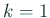
のとき確かに成り立つ。
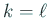 のとき成り立つと仮定して、
のとき成り立つと仮定して、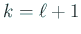 とする。
とする。
 が
が
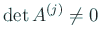 (
(
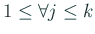 ) を満たすと仮定する。
特に
) を満たすと仮定する。
特に
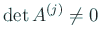 (
(
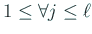 ) であり、
帰納法の仮定より Gauss の消去法の前進消去過程は
) であり、
帰納法の仮定より Gauss の消去法の前進消去過程は 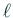 段まで実行できる。
すなわち行に関する基本変形を表す下三角の基本行列の積である
下三角行列
段まで実行できる。
すなわち行に関する基本変形を表す下三角の基本行列の積である
下三角行列 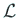 が存在して、
が存在して、
これから
このとき
仮定より
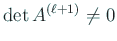
であるから、
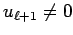
.
ゆえに第
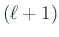
列の対角線より下も掃き出すことができる。
すなわち Gauss の消去法の前進消去過程は
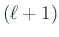
段まで実行できる。


証明.
前半は補題
2.5 から明らか。
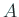
が正則であるならば、
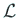
も正則であることに注意して、
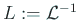
とおけば
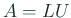
.
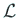
は
単位下三角であるから
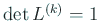
であるので、

.


以上をまとめると、次の定理が得られる。
この定理の、簡単だが応用上重要な系として、次のものがある。
証明.
よく知られているように、対称行列
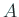
が正値であるためには
が成り立つことが必要十分である。これを思い出せば明らか。


なお、正値対称行列の LU 分解としては、
Cholesky 分解が重要である。
これについては、桂田 [1] などを見よ。
LU 分解の一意性についても片付けておこう。
証明.
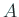
が正則であることから
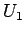
も正則である。
したがって
左辺は単位下三角行列の積であるから単位下三角行列であり、
右辺は上三角行列の積であるから上三角行列である。
ゆえにこの等式の両辺は、単位下三角行列かつ上三角行列であるので、
実は単位行列
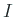
に等しい。これから
が得られる。


とブロック分けすると
これから
これは 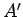 の LU 分解となっているので
の LU 分解となっているので
やり残し「任意の正則行列 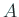 に対して、
ある置換行列
に対して、
ある置換行列 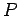 が存在して、
が存在して、
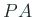 は LU 分解できる」を証明したい。
は LU 分解できる」を証明したい。
桂田 祐史
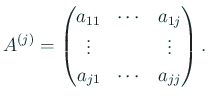
![\begin{jproposition}[主座小行列式$\ne 0$ の必要性]
$n$ 次正方行...
...l k\in\{1,\dots,n\}\quad
\det A^{(k)}\ne 0.
\end{displaymath}\end{jproposition}](img140.gif)
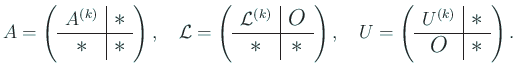
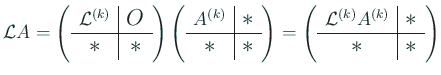
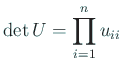 より、
より、
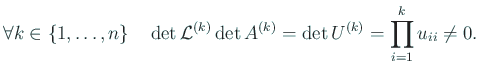
![]() (
(
![]() ) ならば
) ならば ![]() は LU 分解できる
ことを示すには、Gauss の消去法によって具体的に LU 分解を構成してみせる。
は LU 分解できる
ことを示すには、Gauss の消去法によって具体的に LU 分解を構成してみせる。
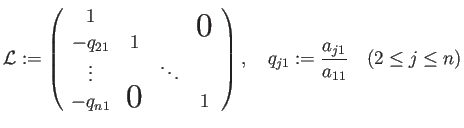
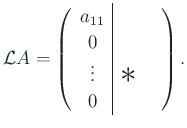
![]() のとき成り立つと仮定して、
のとき成り立つと仮定して、![]() とする。
とする。
![]() が
が
![]() (
(
![]() ) を満たすと仮定する。
特に
) を満たすと仮定する。
特に
![]() (
(
![]() ) であり、
帰納法の仮定より Gauss の消去法の前進消去過程は
) であり、
帰納法の仮定より Gauss の消去法の前進消去過程は ![]() 段まで実行できる。
すなわち行に関する基本変形を表す下三角の基本行列の積である
下三角行列
段まで実行できる。
すなわち行に関する基本変形を表す下三角の基本行列の積である
下三角行列 ![]() が存在して、
が存在して、
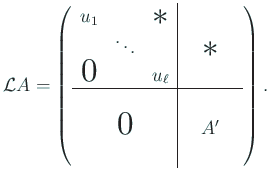
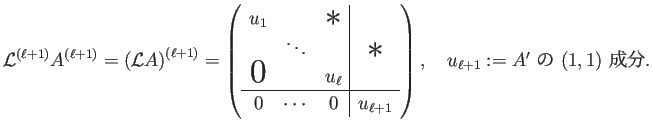
![\begin{jproposition}[主座小行列式$\ne 0$ の十分性]
$n$ 次正方行...
...det A^{(k-1)}}
\quad\mbox{($k=2,\dots,n$)}.
\end{displaymath}\end{jproposition}](img162.gif)




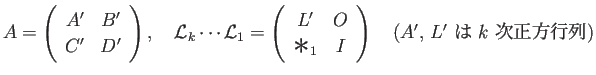
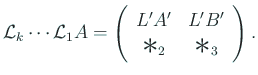
に対して、 ある置換行列
が存在して、
は LU 分解できる」を証明したい。