


Next: 5.3.0.0.1 гВєгГЖгГГгГЧ1
Up: 5 QR ж≥Х
Previous: 5.2 QR е§ЙжПЫ
и°МеИЧ 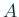 гБМдЄОгБИгВЙгВМгБЯгБ®гБНгАБ
гБМдЄОгБИгВЙгВМгБЯгБ®гБНгАБ
гБ® QR е§ЙжПЫгВТзє∞гВКињФгБЩгБ®гАБ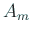 гБЃеѓЊиІТзЈЪгБЃдЄЛеБігБЃжИРеИЖгБѓгБЩгБєгБ¶ 0
гБЂеПОжЭЯгБЩгВЛгАВ
гБЃеѓЊиІТзЈЪгБЃдЄЛеБігБЃжИРеИЖгБѓгБЩгБєгБ¶ 0
гБЂеПОжЭЯгБЩгВЛгАВ
![\begin{jremark}[гБЯгБЊгБЂгБВгВЛи™§иІ£гВТж≠£гБЩ]\upshape
гБУгБЃгБУгБ®гВТгАМ$A_k$...
...\infty} A_k=U
\end{displaymath}гБ®гБ™гВЛгВПгБСгБІгБѓгБ™гБДгАВ \qed
\end{jremark}](img326.gif)
дЄАиИђжАІгБЃињљж±ВгБѓгБїгБ©гБїгБ©гБЂгБЧгБ¶гАБжђ°гБЃеЃЪзРЖгВТи®ЉжШОгБЧгВИгБЖгАВ

и®ЉжШО.

Subsections



Next: 5.3.0.0.1 гВєгГЖгГГгГЧ1
Up: 5 QR ж≥Х
Previous: 5.2 QR е§ЙжПЫ
ж°ВзФ∞ з•РеП≤
2015-12-22
![]() гБМдЄОгБИгВЙгВМгБЯгБ®гБНгАБ
гБМдЄОгБИгВЙгВМгБЯгБ®гБНгАБ
![\begin{jremark}[гБЯгБЊгБЂгБВгВЛи™§иІ£гВТж≠£гБЩ]\upshape
гБУгБЃгБУгБ®гВТгАМ$A_k$...
...\infty} A_k=U
\end{displaymath}гБ®гБ™гВЛгВПгБСгБІгБѓгБ™гБДгАВ \qed
\end{jremark}](img326.gif)
![\begin{jtheorem}[QR ж≥ХгБЃеОЯзРЖ]\upshape
$A\in GL(n;\C)$\ гБІгАБгБЭгБЃеЫЇжЬЙеА...
...ТжИРеИЖгБѓ $\lambda_1$, $\cdots$, $\lambda_n$\ гБЂеПОжЭЯгБЩгВЛгАВ
\end{jtheorem}](img327.gif)
