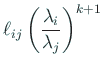


Next: 5.3.0.0.3 ステップ3
Up: 5.3 QR 法の原理
Previous: 5.3.0.0.1 ステップ1
(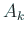 の挙動)
の挙動)
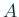 は固有値がすべて相異なるから対角化が可能である。
すなわち
は固有値がすべて相異なるから対角化が可能である。
すなわち
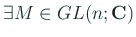 s.t.
s.t.
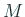 を
を 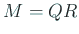 と QR 分解、
と QR 分解、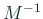 を
を 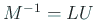 (ただし
(ただし 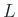 の対角成
分はすべて
の対角成
分はすべて 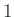 ) と LU 分解して、
) と LU 分解して、
|
(11) |
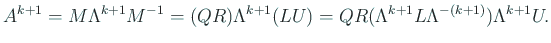 |
ここで
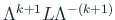 は下三角行列で、対角成分はすべて
は下三角行列で、対角成分はすべて
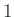 に等しく、
に等しく、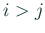 のとき
のとき 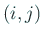 成分は
成分は
に等しい (ただし 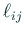 は
は 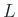 の
の 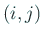 成分)。そこで
成分)。そこで
とおくと、
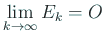 .
上式を (11) 代入して、
.
上式を (11) 代入して、
この
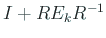 を QR 分解する:
を QR 分解する:
|
(13) |
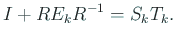 |
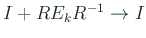 (
(
 ) で、QR 分解の連続性は明らかだから、
) で、QR 分解の連続性は明らかだから、
(13) を (12) に代入して、
|
(14) |
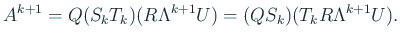 |
この右辺は unitary 行列と、上三角行列の積の形になっている。



Next: 5.3.0.0.3 ステップ3
Up: 5.3 QR 法の原理
Previous: 5.3.0.0.1 ステップ1
桂田 祐史
2015-12-22