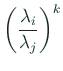


Next: 5.4 QR 分解のアルゴリズム
Up: 5.3 QR 法の原理
Previous: 5.3.0.0.3 ステップ3
(10) と
(15) から
より
この行列は (右辺に注目することで) 上三角行列で、かつ対角線上に
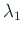 ,
, 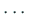 ,
, 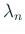 がこの順にならんでいる。
がこの順にならんでいる。
 のとき、
のとき、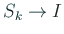 だから
だから
この右辺は上三角行列で、対角成分は 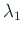 ,
, 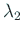 ,
, 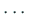 ,
,
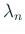 である。
である。
この定理から
 とするときの収束の速さは
とするときの収束の速さは
という因子に関わることが分かる。

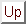


Next: 5.4 QR 分解のアルゴリズム
Up: 5.3 QR 法の原理
Previous: 5.3.0.0.3 ステップ3
桂田 祐史
2015-12-22
![]() とするときの収束の速さは
とするときの収束の速さは