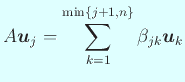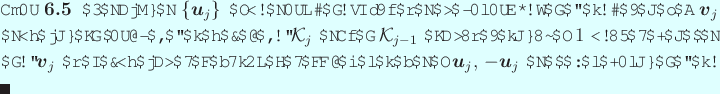иЁјжҳҺ.
д»®е®ҡ
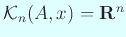
гӮҲгӮҠгҖҒ
(
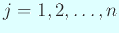
) гҒҢжҲҗгӮҠз«ӢгҒӨгҒ®гҒ§гҖҒ
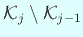
гҒҜз©әгҒ§гҒӘгҒҸгҖҒ
Gram-Schmidt гҒ®зӣҙдәӨеҢ–жі•гҒ«гӮҲгӮҠ
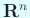
гҒ®жӯЈиҰҸзӣҙдәӨеҹәеә•гҒҢеҫ—гӮүгӮҢгӮӢгҖӮ
гҒҫгҒҹдҪңгӮҠж–№гҒӢгӮүжҳҺгӮүгҒӢгҒ«д»»ж„ҸгҒ®
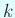
гҒ«еҜҫгҒ—гҒҰ
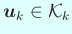
,
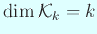
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
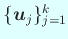
гҒҜ
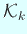
гҒ®еҹәеә•гҒ«гҒӘгҒЈгҒҰгҒ„гӮӢгҖӮ
гҒ•гҒҰгҖҒд»»ж„ҸгҒ® 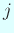 гҒ«еҜҫгҒ—гҒҰгҖҒ
гҒ«еҜҫгҒ—гҒҰгҖҒ
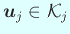 гҒ§гҒӮгӮӢгҒ®гҒ§гҖҒ
гҒ§гҒӮгӮӢгҒ®гҒ§гҖҒ
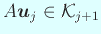 гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
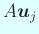 гҒҜ
гҒҜ
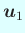 ,
,
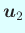 ,
, 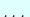 ,
,
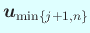 гҒ®з·ҡеҪўзөҗеҗҲгҒ«гҒӘгӮӢгҖӮ
гҒҷгҒӘгӮҸгҒЎ
гҒ®з·ҡеҪўзөҗеҗҲгҒ«гҒӘгӮӢгҖӮ
гҒҷгҒӘгӮҸгҒЎ
гӮ’гҒҝгҒҹгҒҷ
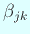
(
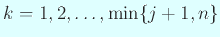
) гҒҢеӯҳеңЁгҒҷгӮӢгҖӮ
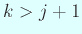
гҒ«еҜҫгҒ—гҒҰ
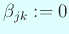
гҒЁгҒҠгҒ„гҒҰгҖҒ
иЎҢеҲ—
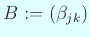
гӮ’е®ҡгӮҒгӮӢгҒЁгҖҒ
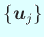
гҒҢжӯЈиҰҸзӣҙдәӨеҹәеә•гҒ§гҒӮгӮӢгҒ“гҒЁгҒӢгӮү
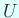
гҒҜе®ҹзӣҙдәӨиЎҢеҲ—гҒ§
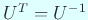
.
гҒ“гӮҢгӮ’дёҠгҒ®зӯүејҸгҒ®дёЎиҫәгҒ«е·ҰгҒӢгӮүгҒӢгҒ‘гҒҰ
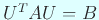
.
гӮӮгҒ—гӮӮ
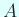
гҒҢе®ҹеҜҫз§°гҒ§гҒӮгӮҢгҒ°гҖҒ
гҒҷгҒӘгӮҸгҒЎ
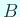
гӮӮеҜҫз§°гҒ§гҒӮгӮӢгҖӮ
еҜҫз§°гҒӘ Hessenberg иЎҢеҲ—гҒҜдёүйҮҚеҜҫи§’иЎҢеҲ—гҒ«д»–гҒӘгӮүгҒӘгҒ„гҖӮ


![]() , гҒҷгҒӘгӮҸгҒЎ
, гҒҷгҒӘгӮҸгҒЎ

![]() гҒ«еҜҫгҒ—гҒҰгҖҒ
гҒ«еҜҫгҒ—гҒҰгҖҒ
![]() гҒ§гҒӮгӮӢгҒ®гҒ§гҖҒ
гҒ§гҒӮгӮӢгҒ®гҒ§гҖҒ
![]() гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
![]() гҒҜ
гҒҜ
![]() ,
,
![]() ,
, ![]() ,
,
![]() гҒ®з·ҡеҪўзөҗеҗҲгҒ«гҒӘгӮӢгҖӮ
гҒҷгҒӘгӮҸгҒЎ
гҒ®з·ҡеҪўзөҗеҗҲгҒ«гҒӘгӮӢгҖӮ
гҒҷгҒӘгӮҸгҒЎ