9 楽器の音の分析と合成

ピアノ、太鼓、鐘などの実際の楽器の音とシミュレートした音を比較する。

楽器の音は、大ざっぱに言うと波動方程式の問題である。 ピアノの場合、第1近似としては弦 (ピアノ線) の振動で、 1次元波動方程式で記述する問題であり、 太鼓の場合、第1近似としては皮 (膜) の振動で、 円盤領域における2次元波動方程式で記述する問題である。

2次元の線形波動方程式

$$\frac{1}{c^2}\frac{\rd^2 u}{\rd t^2} =\frac{\rd^2 u}{\rd x^2}+\frac{\rd^2 u}{\rd y^2}$$

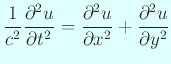
は、数学的には理論解も知られているが、 円形膜のような単純な場合でもBessel 関数のような特殊関数が必要になり、 それなりに難しい。 数値計算的にも、上で書いたような困難さがあり、挑戦的な課題である。

ピアノの音は1次元の振動なので簡単なように思われる。 しかし詳しく調べてみるとインハーモニシティと呼ばれる現象があり (太田 [71], 土橋 [71])、 決して単純な1次元線形波動方程式

$$\frac{1}{c^2}\frac{\rd^2 u}{\rd t^2} =\frac{\rd^2 u}{\rd x^2}$$

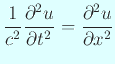
で記述できるものではないことが分かる。

音響や機械関係の学会で、方程式に修正 (ただしあくまで線形) を加えることで、 実際の現象を説明する試みがなされているようである (例えば引地・小坂 [49], 橋本・梅谷 [71])。

$$\frac{\rd^2 u}{\rd t^2}=\frac{T}{\sigma}\frac{\rd^2 u}{\rd x^2} ... ...}{\rd x^4} -2b_1\frac{\rd u}{\rd t}+2b_3\frac{\rd^3 u}{\rd t^3} +f(x,x_0,t),$$

$$F_H(t)= \left\{ \begin{array}{ll} K\left\vert\eta(t)-u(x_0,t)\rig... ...xt{$\eta(t)\ge u(x_0,t)$}\ 0 & \text{$\eta(t)< u(x_0,t)$}, \end{array} \right.$$

$$M_H\frac{\D^2\eta}{\D t^2}=-F_H(t),$$

$$f(x,x_0,t)=\frac{F_H(t)g(x,x_0)} {\sigma\int_{x_0-\delta x}^{x_0+\delta x}g(x,x_0)\D x}.$$

$$u(0,t)=u(L,t)=0,\quad \frac{\rd^2 u}{\rd x^2}(0,t)=\frac{\rd^2 u}{\rd x^2}(L,t)=0.$$

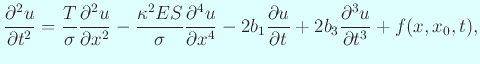
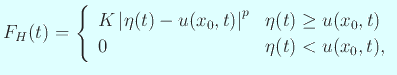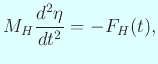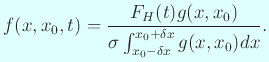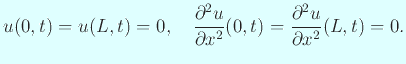
「コンピュータ音楽 関係論文一覧」 を見よ。

一方で、弦の振動を素直にモデル化すると、

$$\frac{1}{c^2}\frac{\rd^2 u}{\rd t^2}= \frac{\rd}{\rd x} \left( \frac{u_x}{\sqrt{1+u_x^2}} \right)$$

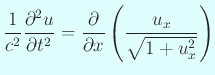
のような非線型波動方程式が得られる。 これについて数学的な研究はほとんど進んでない (らしい)。 数値計算することはそれほど困難があるとは考えられないので (プログラムを書くだけならば実行した先輩がいる)、 この数値シミュレーションをしてみるのも面白いかもしれない (例えば倍音はどうなる？？)。

楽器の音は、数学村の住人のような実験素人にとっても、 比較的簡単に実際の音を採取して分析するのが簡単という意味で、 実験のやりやすい対象である。 特に2007年度の卒研で基本的なノウハウを蓄積しておいたので、 0からの困難な出発をする必要はない (最近は安価な高性能録音機があるので、原音採取が出来ないものかと思っている)。 数学的にも、離散Fourier変換 (高速Fourier変換)、 Wavelet解析のように、 学ぶに足る話題が目白押しで退屈する暇はないであろう (過去の卒研で Wavelet を学んだ先輩はいないので、一苦労はしそう)。

将来的には、共鳴器を考えた3次元計算まで手がけたいと思っている。

有名なフレッチャー＆ロッシング『楽器の物理学』 [51] という本を まじめに読んで勉強する人が出て来ないだろうか。