![]() を正定数として、
を正定数として、
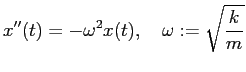
に従うことを学んでいると思う。 これについても、解き方は後回しにして、結果だけを述べておくと
となる (有名なので高校生の時に習ったかもしれない)。
とすると、
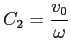 であるので、
であるので、
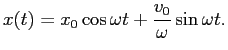
このような問題も Mathematica を使って、前問と同様に解くことが出来る。
sol=x[t]/.DSolve[{x''[t]==-omega^2 x[t],x[0]==x0,x'[0]==v0},x,t]
g=Plot[sol/.{omega->1,x0->1,v0->1},{t,0,20}]
|