5.2 単振り子の方程式

単振り子の運動は、鉛直線から測った振れの角度 $\theta (t)$ について、

$$\theta''(t)=-\frac{g}{\ell}\sin\theta(t)$$ (7)

という微分方程式を満たす。ここで $g$ は重力加速度、 $\ell$ は振り子の長さである。入門段階の物理では、通常は、微小振動の場合、 $\theta\kinji\sin\theta$ であるとして、

$$\theta''(t)=-\omega^2\theta(t),\quad \omega:=\sqrt{\frac{g}{\ell}}$$

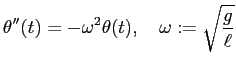
という単振動方程式で近似して議論する (これから近似的に周期運動であり、 周期が 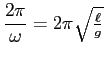$\dfrac{2\pi}{\omega} =2\pi\sqrt{\frac{\ell}{g}}$ であることが分かる)。

近似をしないで (7) の解を得るのはちょっと難しい。 一応書くだけ書いておくと、 $k\in(0,1]$ として、初期条件

$$\theta(0)=0,\quad \theta'(0)=2k\omega$$ (8)

を与えた初期値問題の解は

$$\theta(t)=2\sin^{-1}\left(k\;\mathrm{sn}(\omega t,k)\right).$$ (9)

ただし $\mathrm{sn}$ は Jacobi の楕円関数である²(桂田 [3])。

こうしてとりあえずは、解を「既知の」関数を使って表すことが出来たが ($\sin^{-1}$ を習ったばかりで、 $\mathrm{sn}$ なんて「既知」と言われても困るという人がいるかもしれないが…)、 いざ解の数値を求めたり、解を図示しようとすると、 コンピューターの助けでも借りないと、 $\sin^{-1}$ や $\mathrm{sn}$ の計算が出来ないことに気づく (特に $\mathrm{sn}$ の計算にはコンピューターがあっても結構手こずる)。 解の数値が知りたい場合や、解のグラフが描きたい場合、 (9) を使う方法は、 後述する数値解を使う方法と比べて、特に優れているとは言えないのである。

初期値問題の解を微分方程式の数値解法で求めるのは簡単である。 数値解法の詳細については、そのうち学ぶ機会があると思われるが、 ここでは Mathematica にやらせてみよう。 これまでと同様に

DSolve[] では解けない

sol=DSolve[{x''[t]==-Sin[x[t]], x[0]==0, x'[0]==1.6},x,t]

としても、残念ながら解は得られない。 DSolve[] の代わりに NDSolve[], t の代わりに {t,0,10} とする。

NDSolve[] で解ける

sol=NDSolve[{x''[t] == -Sin[x[t]], x[0] == 0, x'[0] == 1.6}, x, {t, 0, 10}]

ただし、結果は式の形では得られず、 InterpolatingFunction (Mathematica 用語) というもので、 そのままでは正体が分からない。グラフ表示をしてみよう。

g1=Plot[x[t] /. sol,{t,0,10}]
g2=ParametricPlot[{x[t],x'[t]} /. sol,{t,0,10}]

とすれば計算した解の表示が得られる。

図 4: 横軸 $t$ , 縦軸 $\theta (t)$

図 5: 横軸 $\theta (t)$ , 縦軸 $\theta '(t)$