... CLASS="textbf">MuPAD¹

ずっと以前は、 個人・非商用利用には無償で利用できるバージョンがありましたが、 今では MATLAB に取り込まれました。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... CLASS="textbf">REDUCE²

筆者が学生の頃 (三十ん年前)、 大型計算機で REDUCE を使って、 計算するのがおしゃれだった。 今ではフリーソフトになっている。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Risa/Asir³

Made in Japan. グレブナー基底の計算など得意です。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Macsyma⁴

かつて MIT でしか使えなかった 憧れの (歴史的) 処理系。 古い本を読むと良く出て来ます。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...MAXIMA⁵

Macsyma の子孫。 GPL (GNU GENERAL PUBLIC LICENSE) で配布されている (ゆえに、 いわゆるフリーソフト)。メジャーになれるか？？

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... は不自由な言語であると言えます⁶

もちろん 不自由さを補って余りある大きな利点があるから、 現在でも盛んに使われているわけです。 例えば、実際の処理系の (反復の多い) 数値計算の速さで比べると C が圧勝します。 原理的には一つのプログラミング言語があれば、 どんな計算でも出来るはずなのですが、 実際的な意味で万能のプログラミング言語と呼べるものは存在せず、 適材適所を心がけることが重要です。 みなさんも、あまり一つの言語、一つのシステムにこだわらずに、 機会があったら色々なものを勉強してみましょう。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 計算結果は表示されない⁷

意味がないように思うかも知れないが、 a=2^1000 のような変数への代入など、 副作用のある処理をする場合に使うことがある。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (これは右結合⁸

a^ b^c は $a^{b^c}=a^{(b^c)}$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

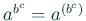... 分数式の約分⁹

共通因数を約する。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 次元波動方程式を解くための有名な変数変換の例の確認です¹⁰

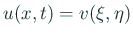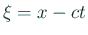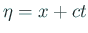$u(x,t)=v(\xi,\eta)$ , $\xi=x-c t$ , $\eta=x+c t$ とするとき、 $\dfrac{1}{c^2}\dfrac{\rd^2 u}{\rd t^2}-\dfrac{\rd^2 u}{\rd x^2} =-4\dfrac{\rd^2 v}{\rd\xi\rd\eta}$ .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

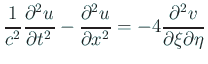... (知らぬ間に¹¹

自分が作成した関数で、 Mathematica の組み込み関数を使っていて、 それがリスト対応だったりすると、 自作の関数も自然とそうなったりすることがあります。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...ContourPlot[]¹²

等高線のことを contour (line) と呼ぶ。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... が用意されている¹³

密度、 濃度を density と呼ぶ。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
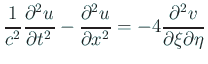