- ...
いわば行列の等比数列1
- 点の列は点列と言うから、
行列の列は行列列?そういう本はないみたいです。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
掃き出し法を改良したものである2
- 見方によっては、
ガウスの消去法は中学校で習う加減法 (初めて習う連立1次方程式の解法!)
そのものであり、
大学の線形代数で習う解法は、実用性では退化していると言えなくもない (?)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 回の乗除算で十分である3
- 計算にどれくらい手間がかかるかを計るために、
基本的な演算の回数を数えるという方法がある。
しばしば、
四則演算のそれぞれについて数える代りに、
乗除算の回数だけを数えて目安にする、という手段が採用される
(4次元ベクトルよりは1つの数値が分かりやすい)。
もう少し詳しいことが知りたければ、
例えば桂田 [] を見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
けることになる4
- 細かい話をすると、
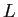 の対角成分が
の対角成分が 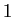 である場合は、
割り算の回数が
である場合は、
割り算の回数が 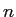 回減って、
回減って、
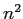 回の乗除算で解けることになる。
逆行列を知っている場合、
連立1次方程式は
回の乗除算で解けることになる。
逆行列を知っている場合、
連立1次方程式は 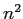 回の掛け算で解けるが、
それとまったく互角であることが分かる。
回の掛け算で解けるが、
それとまったく互角であることが分かる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.