A..1 Gaussの消去法

(他の授業で習ったのではないか？と思うけれど、 念のため。)

連立 $1$ 次方程式の解法として、線形代数の教科書には クラーメ ル (Cramer) の公式や掃き出し法 (ヨルダン Jordan の消去法ともいう) が 説明されていることが多いが、 Gaussの消去法は、 掃き出し法を改良したものである²。

例として次の方程式を取りあげて説明しよう。

$$\left\{ \begin{array}{rcrcrl} 2x_1&+&3x_2&-&x_3&=5 4x_1&+&4x_2&-&3x_3&=3 -2x_1&+&3x_2&-&x_3&=1. \end{array} \right.$$ (1)

掃き出し法では係数行列と右辺のベクトルを並べた行列を作り、それに

1. ある行に 0 でない定数をかける。
2. 2つの行を入れ換える。
3. ある行に別の行の定数倍を加える。

のような操作 -- 行に関する基本変形と呼ぶ -- をほどこして、 連立方程式の係数行列に相当する部分を単位行列にするのであった。

$$\left( \begin{array}{cccc} 2&3&-1&5 \\ 4&4&-3&3 \\ -2&3&-1&... ...}{2}&\frac{5}{2} \\ 0&-2&-1&-7 \\ 0&6&-2&6 \end{array} \right)\rightarrow$$

$$\rightarrow \left( \begin{array}{cccc} 1&\frac{3}{2}&-\frac{1}... ...\\ 0&1&\frac{1}{2}&\frac{7}{2} \\ 0&0&1&3 \end{array} \right) \rightarrow$$

$$\rightarrow \left( \begin{array}{cccc} 1&0&0&1 \\ 0&1&0&2 \\... ...array} \right) =\left( \begin{array}{c} 1\\ 2\\ 3 \end{array} \right).$$

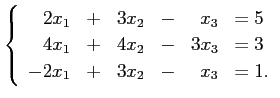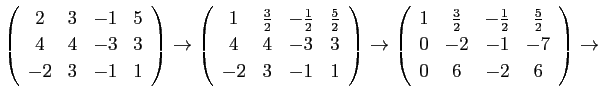
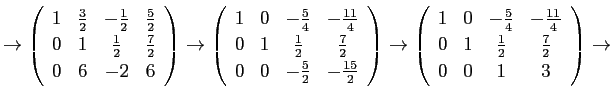
Gauss の消去法も、前半の段階はこの方法に似ていて、 同様の変形を用いて掃き出しを行なうのだが、 以下のように対角線の下側だけを 0 にする。

$$\left( \begin{array}{cccc} 2&3&-1&5 \\ 4&4&-3&3 \\ -2&3&-1&... ...n{array}{cccc} 2&3&-1&5 \\ 0&-2&-1&-7 \\ 0&0&-5&-15 \end{array} \right).$$

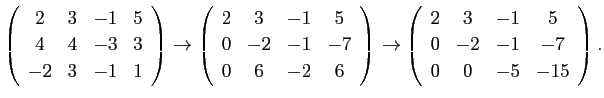
最後の行列は

$$2x_1+3x_2-x_3 =5,$$

$$-2x_2-x_3 =-7,$$

$$-5x_3 =-15$$

ということを表しているので、下の方から順に

$$x_3=\frac{-15}{-5}=3, \quad x_2=\frac{-7+x_3}{-2}=2, \quad x_1=\frac{5-3x_2+x_3}{2}=\frac{5-3\times 2+3}{2}=1$$

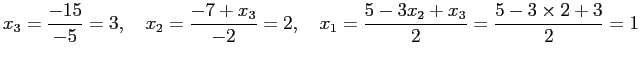
と解くことが出来る。前半の対角線の下側を 0 にする掃き出しの操作を 前進消去 (forward elimination)、後半の代入により解の値を求める 操作を後退代入 (backward substitution) と呼ぶ。

以下簡単に $3$ つの方法の比較をしよう。

クラーメルの公式を適用するには $n+1$ 個の行列式を求める必要があるため、 計算の手間がかかる (大きな計算量が必要になる、という)。実際、 行列式を一つ計算するための手間は、 連立方程式を一つ解くための手間と本質的に同等であることが分かっているので、 クラーメルの公式を使うことに固執すると、 本来必要な計算量の $n$ 倍程度の計算をする羽目になり、 $n$ が大きい場合には、大変な損をすることになる。 そのため、実際の数値計算では、ごく特殊な例を除いて、 クラーメルの公式が利用されることはない。クラーメルの公式は、 理論的な問題を扱う場合に、真価が発揮されるものである。

このクラーメルの方法に比べれば、掃き出し法は、 かなりの実用性を持っているが、 多くの微分方程式の数値計算に現れる疎行列の場合には、 Gauss の消去法の方が断然有利である。 それは、Gauss の消去法を採用すると、 掃き出しの途中に現れる行列が疎行列のままであることから、 計算量が少なくてすむためである。