

Next: A..3 Gauss の消去法は LU
Up: A. 前回の後始末
Previous: A..1 Gaussの消去法
連立1次方程式を解くのに、逆行列を一度計算してしまえば、後は楽じゃない?
という考えに「それは勘違いです。LU 分解を使うべきです。」ということを、
以下の数小節を費やして説明する。
対角線より上にあるすべての成分が 0
であるような行列を
下三角行列と呼ぶ。
すなわち
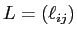 が下三角行列であるとは、
が下三角行列であるとは、
が成り立つことをいう。
同様に対角線より下にあるすべての成分が 0
である行列を
上三角行列と呼ぶ。
正則な下三角行列の全体は乗法に関して群をなす。
上三角行列についても同様である。
行列 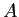 に対して、
に対して、
をみたす 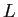 ,
, 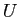 が存在するとき、
が存在するとき、
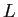 と
と 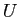 の組を
の組を 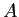 の LU 分解とよび、
の LU 分解とよび、
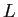 と
と 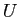 の組を求めることを
の組を求めることを 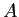 を LU 分解する、という。
を LU 分解する、という。
- 与えられた正則行列
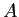 が LU 分解を持つためには、
が LU 分解を持つためには、
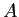 のすべての首座小行列式
のすべての首座小行列式 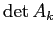 が 0
でないことが必要十分である。
が 0
でないことが必要十分である。
- 任意の正則行列
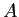 に対して、適当に行の交換を行った行列
に対して、適当に行の交換を行った行列 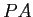 は、
LU 分解を持つ
(
は、
LU 分解を持つ
(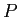 はいわゆる置換行列で、左からかけることで行の交換がおこる)。
はいわゆる置換行列で、左からかけることで行の交換がおこる)。


Next: A..3 Gauss の消去法は LU
Up: A. 前回の後始末
Previous: A..1 Gaussの消去法
桂田 祐史
2012-07-11
![]() が下三角行列であるとは、
が下三角行列であるとは、
![]() に対して、
に対して、