- ... B. Pascal1
- Blaise Pascal (1623-1662, フランスに生
まれる). 円錐曲線の Pascal の定理, 計算器の発明 (1642), 流体静力学の基
礎 (「自然は真空を嫌う」をしりぞける、Pascal の原理), Fermat との手紙
で確率について議論 (Pascal の三角形, 数学的帰納法)、僧院に入って余生を
過ごす。遺著 Pensées は有名 (「人間は考える葦である」)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Fermat2
- Pierre de Fermat (1601-1665, フランスに生まれる). 役
所の職員。余暇に数学を研究、成果は書簡中に発表する。数論の研究 (Fermat
予想), 解析幾何学をはじめて微積分学の先駆, 光学における Fermat の原理
など。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...との往復書簡でトランプ賭博3
- サイコロ賭博であるという説
もある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... P. S. Laplace4
- Pierre Simon Laplace (1749-1827, フランスに生
まれる). 解析学を天体力学 (太陽系の起源に関する Kant-Laplace の星雲説),
ポテンシャル論, 確率論に応用して華々しい結果を得た。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... と表わすようにすると5
- テキストでは、
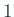の目が出ることは [1em]1 と表わしているが、
面倒なので箱抜きで表わす
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...同様に確からしい6
- 「同様に確からしい」というのは、
最初は厳密な定義のない呪文みたいなものだが、いったん確率が定義されると、
「同様に確からしい」根元事象の確率はみな等しくなる。つまり「同様に確か
らしい」=「確率が等しい」と考えて良い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...加法定理
7
- この講義の話の筋としては、定理というよりは、公理である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
できる8
- ベン図は便利だが、それで証明になるかというと、微妙であ
る。「一般の」場合の図を描かなければいけないが、図が一般であるかどうか、
どうやれば保証できるのだろう？特に複雑な場合ではベン図を描くのも難しい。
ただし発見的な考察には便利である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(normal9
- 数学の分野で normal (数学分野では「正規」と訳される) と
いう語を与えられるものは、かなり重要で根本的なものに限られる。
似たような言葉に regular (数学分野では「正則」と訳される) というのがあるが、
それよりも一段上の存在である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gauss10
- K. F. Gauss は、
近世までの三大数学者に数えられる大数学者である。
10代のうちに小惑星セレスの軌道計算などで名を上げたように
数学以外の業績も大きいが (例えば電磁気学の Gauss の法則、
地磁気の研究など)、
正17角形の定木とコンパスによる作図法の発見を果たした後は、
数学を専門とした。
「任意の
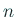次代数方程式は複素数の範囲で 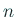個の根を持つ」
と言う代数学の基本定理の証明、
平方剰余の相互法則の発見、
複素関数論の先駆的研究 (発表せず)、
非ユークリッド幾何の発見 (発表せず)、
微分幾何学の先駆的研究 (曲率の導入、
「球面の正確な地図を平面上に作ることは不可能である」ことの証明など)、
数値計算法の先駆的研究 (Gauss の消去法、Gauss-Jordan 法、
Gauss-Seidel 法などの反復法、Gauss の数値積分則) など、
山のような一級の業績がある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.