Next: 2.2.2 1ж¬Ўе…ғгҒ®е ҙеҗҲгҒ®жңүйҷҗиҰҒзҙ жі• Up: 2.2.1 1ж¬Ўе…ғгҒ®е ҙеҗҲгҒ®ејұи§ЈгҒ®ж–№жі• Previous: 2.2.1 1ж¬Ўе…ғгҒ®е ҙеҗҲгҒ®ејұи§ЈгҒ®ж–№жі•
![$\displaystyle -\left[u'(x)v(x)\right]_0^1+\int_0^1 u'(x)v'(x)\;\Dx=
\int_0^1 f(x)v(x)\;\Dx.
$](img66.png)
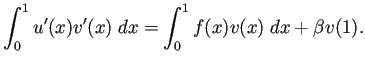
![]()
ж¬ЎгҒ«еӨүеҲҶе•ҸйЎҢ3(variational problem) гҒ«гҒ—гҒҹгӮӮгҒ®гӮ’иҝ°гҒ№гӮӢгҖӮ
| е•ҸйЎҢ (V) |
|
![$\displaystyle J[u]:=\frac{1}{2}\int_0^1 u'(x)^2\Dx-
\int_0^1 f(x)v(x)\;\Dx-\beta v(1).
$](img74.png)
|
![]() гҒҢжұҺй–ўж•°гҒ§гҒӮгӮӢгҒ“гҒЁгҒ«жіЁж„ҸгҒ—гӮҲгҒҶгҖӮ
гҒҢжұҺй–ўж•°гҒ§гҒӮгӮӢгҒ“гҒЁгҒ«жіЁж„ҸгҒ—гӮҲгҒҶгҖӮ
(W) гҒЁ (V) гҒҜеҗҢеҖӨгҒӘе•ҸйЎҢгҒ§гҒӮгӮҠгҖҒ еёёгҒ«дёҖж„Ҹзҡ„гҒӘи§ЈгӮ’жҢҒгҒӨгҒ“гҒЁгҒҢжҜ”ијғзҡ„е®№жҳ“гҒ«еҲҶгҒӢгӮӢгҖӮ

йҖҶгҒ« ![]() гҒҢгҒӮгӮӢзЁӢеәҰж»‘гӮүгҒӢгҒ§гҒӮгӮҢгҒ°гҖҒ
(W), (V) гҒ®и§ЈгҒҜ (P) гҒ®и§ЈгҒ§гҒӮгӮӢгҒ“гҒЁгҒҢзӨәгҒ•гӮҢгӮӢгҖӮ
гҒҢгҒӮгӮӢзЁӢеәҰж»‘гӮүгҒӢгҒ§гҒӮгӮҢгҒ°гҖҒ
(W), (V) гҒ®и§ЈгҒҜ (P) гҒ®и§ЈгҒ§гҒӮгӮӢгҒ“гҒЁгҒҢзӨәгҒ•гӮҢгӮӢгҖӮ
е•ҸйЎҢ (V) гҒ®и§Ј (гҒқгӮҢгҒҜ (W) гҒ®и§ЈгҒ§гӮӮгҒӮгӮӢ) гҒҢ![]() зҙҡгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’иӘҚгӮҒгӮӢгҒЁгҖҒ
(P), (W), (V) гҒҜдә’гҒ„гҒ«еҗҢеҖӨгҒӘе•ҸйЎҢгҒЁгҒ„гҒҶгҒ“гҒЁгҒ«гҒӘгӮӢгҖӮ
(W)
зҙҡгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’иӘҚгӮҒгӮӢгҒЁгҖҒ
(P), (W), (V) гҒҜдә’гҒ„гҒ«еҗҢеҖӨгҒӘе•ҸйЎҢгҒЁгҒ„гҒҶгҒ“гҒЁгҒ«гҒӘгӮӢгҖӮ
(W) ![]() (P) гҒҜгҖҒDirichlet еҺҹзҗҶгҒ®дёҖиҲ¬еҢ–гҒ§гҒӮгӮӢ
(Laplace ж–№зЁӢејҸгҒ®Dirichletеўғз•ҢеҖӨе•ҸйЎҢгҒ®е ҙеҗҲгҖҒ
гҒ“гҒ®
(P) гҒҜгҖҒDirichlet еҺҹзҗҶгҒ®дёҖиҲ¬еҢ–гҒ§гҒӮгӮӢ
(Laplace ж–№зЁӢејҸгҒ®Dirichletеўғз•ҢеҖӨе•ҸйЎҢгҒ®е ҙеҗҲгҖҒ
гҒ“гҒ® ![]() гҒҜ Dirichlet з©ҚеҲҶ (гҒ®
гҒҜ Dirichlet з©ҚеҲҶ (гҒ®![]() еҖҚ) гҒ«д»–гҒӘгӮүгҒӘгҒ„гҖӮ)гҖӮ
еҖҚ) гҒ«д»–гҒӘгӮүгҒӘгҒ„гҖӮ)гҖӮ
гҒқгҒ“гҒ§е•ҸйЎҢ (P) гӮ’и§ЈгҒҸд»ЈгӮҸгӮҠгҒ«гҖҒ(W) гҒӮгӮӢгҒ„гҒҜ (V) гӮ’и§ЈгҒҸгҒ“гҒЁгӮ’зӣ®жҢҮгҒҷгҖӮ
йҖҡеёёгҖҒеӨүеҲҶжі•гҒҜгҖҒеӨүеҲҶе•ҸйЎҢгӮ’и§ЈгҒҸгҒҹгӮҒгҒ«гҖҒгҒқгӮҢгҒЁеҗҢеҖӨгҒӘеҫ®еҲҶж–№зЁӢејҸгҒ®е•ҸйЎҢгӮ’е°ҺгҒҚгҖҒ гҒқгҒЎгӮүгӮ’и§ЈгҒҸгҒ“гҒЁгҒ§еӨүеҲҶе•ҸйЎҢгҒ®и§ЈгӮ’еҫ—гӮӢгҒ®гҒҢжҷ®йҖҡгҒ§гҒӮгӮӢгҒҢгҖҒ гҒ“гҒ“гҒ§гҒҜйҖҶгҒ«еҫ®еҲҶж–№зЁӢејҸгҒ®е•ҸйЎҢгӮ’и§ЈгҒҸгҒҹгӮҒгҒ«гҖҒгҒқгӮҢгӮ’еӨүеҲҶе•ҸйЎҢгҒ«жӣёгҒҚжҸӣгҒҲгҖҒ гҒқгӮҢгӮ’зӣҙжҺҘи§ЈгҒҸгҖҒгҒЁгҒ„гҒҶжүӢй ҶгҒ®иӯ°и«–гӮ’гҒ—гҒҰгҒ„гӮӢгҖӮ гҒ“гӮҢгҒҜгҖҒеӨүеҲҶжі•гҒ®зӣҙжҺҘжі•гҒЁе‘јгҒ°гӮҢгӮӢгӮӮгҒ®гҒ«гҒӘгҒЈгҒҰгҒ„гӮӢгҖӮ