Next: 2.2.3 2次元の場合の弱解の方法 Up: 2.2 Poisson方程式に対する弱解の方法 Previous: 2.2.1.1 (P) の解が (W)
![]() を
を
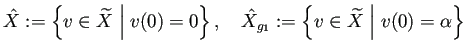
次の2つの問題は同値であり、常に一意的な解 ![]() を持つ。
それを近似解として採用する。
を持つ。
それを近似解として採用する。
| (
|
|
Find
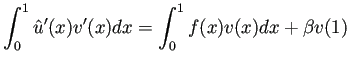 ( (
|
| (
|
|
Find
![$\displaystyle J[\hat u]=\min_{w\in \hat X_{g_1}} J[w].
$](img92.png)
|
![]() を、
を、
![]() ,
,
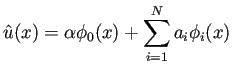
実は ![]() が
が ![]() の
の![]() 等分点であるとき、
有限要素解
等分点であるとき、
有限要素解 ![]() の
の ![]() での値は、差分解
での値は、差分解 ![]() と一致する。
もちろん、いつもそうなるわけではない
(もしそうならば、2つの方法を考える意味がない)。
と一致する。
もちろん、いつもそうなるわけではない
(もしそうならば、2つの方法を考える意味がない)。
有限要素法には以下の利点がある。