Next: 6.3 近似等角写像を求めるための天野の方法 Up: 6 Laplace 方程式に対する基本解の方法 Previous: 6.1.3 Green の積分公式 (続き)
簡単のため、
![]() の場合の Laplace 方程式の境界値問題
の場合の Laplace 方程式の境界値問題
![]() が滑らかな境界を持つ有界領域の場合に、
この境界値問題が一意的な解を持つことは知られている。
が滑らかな境界を持つ有界領域の場合に、
この境界値問題が一意的な解を持つことは知られている。
![]() が (円盤とか、長方形とか) 特別な形をしている場合に、
解
が (円盤とか、長方形とか) 特別な形をしている場合に、
解 ![]() を求める公式はいくつか知られているが、
ここでは多くの場合に使える数値解法を紹介する。
一見素朴であるが、多くの場合に良好な近似解を得ることが出来る。
を求める公式はいくつか知られているが、
ここでは多くの場合に使える数値解法を紹介する。
一見素朴であるが、多くの場合に良好な近似解を得ることが出来る。
![]() の外部に
の外部に![]() を「囲むように」点
を「囲むように」点
![]() を取り、
を取り、
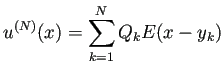
次のような利点がある。
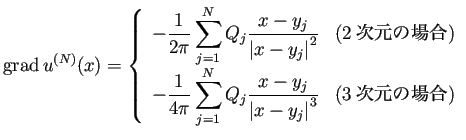
基本解の方法以外に、基本解を利用する方法として、 境界要素法 (boundary element method, BEM) がある。