Next: 5 領域の等角写像, Riemannの写像定理, ポテンシャル問題との関係 Up: ポテンシャル問題とその数値解法 Previous: 3.2 FreeFem++ プログラム (その2)
(この文書は、 2018/6/18 の講義のためのメモ 08-20180618応用複素関数.pdf の主要部分を打ち込んだものである。 次の節と適当にマージする。)
![\begin{jdefinition}
\begin{enumerate}[(1)]
\item
$U$ は $\mathbb{C}$ の領�...
... がともに正則であることをいう。
\end{enumerate}\end{jdefinition}](img138.png)
|
![]() で交わる滑らかな2曲線
で交わる滑らかな2曲線 ![]() ,
, ![]() があるとき、
があるとき、
![]() と
と ![]() がなす角は、
がなす角は、
![]() と
と ![]() を
を ![]() で写した2曲線のなす角に等しい。
実際
で写した2曲線のなす角に等しい。
実際 ![]() で
で ![]() を通る曲線
を通る曲線
![]() に対して、
に対して、
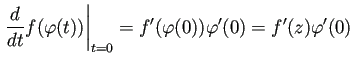
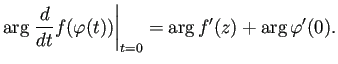
|
|

![\begin{jexample}[単位円盤の等角写像]
$z_0\in D_1$, $\eps\in\mathbb{C}$...
...�定理を用いる。
詳しいことは付録に回す)。 \qed
\end{jexample}](img151.png)

![]()
数学の多くの分野で「同型写像」と呼ばれる写像があるが、
双正則写像は複素関数論における同型写像と言って良いであろう。
![]() が双正則であるとき、
複素関数論的には
が双正則であるとき、
複素関数論的には ![]() と
と ![]() は同じ、ということである。
は同じ、ということである。
これは応用上も意味があることで、
例えば ![]() (
(![]() ) における渦無し非圧縮流は、
) における渦無し非圧縮流は、![]() (
(![]() ) によって
) によって
![]() (
(![]() ) における渦無し非圧縮流にうつる。
) における渦無し非圧縮流にうつる。
![]() と
と ![]() の一方で流れの問題が解ければ、他方でも解けたことになる、等々。
の一方で流れの問題が解ければ、他方でも解けたことになる、等々。
同型写像というものを考えると、標準的なものに移すことが問題になるが、 複素関数論では、次の定理が基礎的である。
記号の紹介
複素平面の原点中心、半径 ![]() の開円盤を
の開円盤を ![]() で表す:
で表す:
![]() .
.
|
|
![]() のことを
のことを ![]() の等角写像、
の等角写像、![]() の写像関数と呼ぶことがある。
(要するに、
「
の写像関数と呼ぶことがある。
(要するに、
「![]() の等角写像」とは、
の等角写像」とは、![]() から
から ![]() への双正則な関数のことである。)
への双正則な関数のことである。)
![\begin{jremark}
\begin{enumerate}[(1)]
\item
条件 $U\ne\mathbb{C}$ は必要...
...�数である($U$のmodulusと呼ばれる)。 \qed
\end{enumerate}\end{jremark}](img162.png)
上の定理の仮定のもとで、双正則写像 ![]() は一意的には定まらないが、
次の定理が成り立つ。
は一意的には定まらないが、
次の定理が成り立つ。
![\begin{jproposition}[等角写像の正規化条件]
$U$ は $\mathbb{C}$ 内...
...�像 $\varphi\colon U\to D_1$ が一意的に存在する。
\end{jproposition}](img163.png)
|
条件 (5.1) を正規化条件と呼ぶ。
複素平面
![]() 内の任意の単純閉曲線 (Jordan曲線)
内の任意の単純閉曲線 (Jordan曲線) ![]() は、
ある有界領域
は、
ある有界領域 ![]() を「囲む」が、
を「囲む」が、![]() は単連結である。
こういう
は単連結である。
こういう ![]() を Jordan 領域と呼ぶ。
この場合は、
任意の双正則函数
を Jordan 領域と呼ぶ。
この場合は、
任意の双正則函数
![]() に対して、
同相写像であるような拡張
に対して、
同相写像であるような拡張
![]() が存在することが知られている
(Carathéodry の定理)。
が存在することが知られている
(Carathéodry の定理)。
その場合は、
ポテンシャル問題を解くことで![]() が求まることを説明しよう。
が求まることを説明しよう。
![]() となる
となる
![]() を取ると、
関数
を取ると、
関数
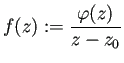 は
(
は
(![]() が除去可能特異点であるので)
が除去可能特異点であるので) ![]() で正則である。
で正則である。
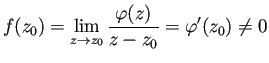
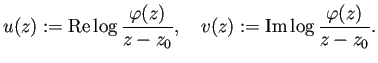
| (4.1) |
| (4.2) |
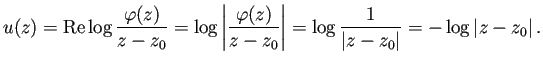
| (4.3) |
これはポテンシャル問題であり、解が一意的に存在する。
こうして ![]() が定まるが、
が定まるが、
![]() は
は ![]() の共役調和関数として定数差を除き定まる。
特に
の共役調和関数として定数差を除き定まる。
特に ![]() を満たすものを選ぶ。
を満たすものを選ぶ。
このとき
桂田 祐史