Next: 5.4 Ť™§Ś∑ģ„ĀģÁČĻśÄßťĖĘśēį„Āģšĺč (2) ÁĄ°ťôźŚĆļťĖď„ĀģŚŹįŚĹĘŚÖ¨ŚľŹ Up: 5 śēįŚÄ§Á©ćŚąÜ„Āģťęėś©č„ÉĽś£ģ„Āę„āą„ā荙§Ś∑ģŤß£śěźÁźÜŤęĖ Previous: 5.2 śúČÁźÜťĖĘśēį„ĀģÁ©ćŚąÜ„Āł„ĀģŚŅúÁĒ®
![]() ,
, ![]() „ĀģŚ†īŚźą„Āģ
„ĀģŚ†īŚźą„Āģ ![]() ÁāĻŤ§áŚźą„ā∑„É≥„Éó„āĹ„É≥ŚÖ¨ŚľŹ
ÁāĻŤ§áŚźą„ā∑„É≥„Éó„āĹ„É≥ŚÖ¨ŚľŹ ![]()
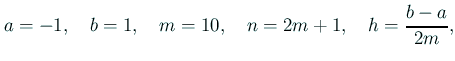
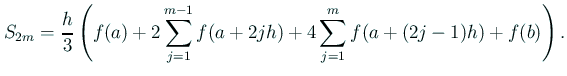
„Āď„āĆ„ĀĮ
![$\displaystyle w_k=
\left\{
\begin{array}[tb]{ll}
h/3 & \text{($k=0,2m$)} ...
...ots,m-1$)} \\
4h/3 & \text{($k=2j-1$, $j=1,2,\dots,m$)}
\end{array} \right.
$](img254.gif)
„Ā®„Āä„ĀŹ„Ā®„ÄĀ
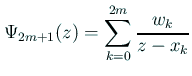
„Ā®śõł„ĀĎ„āč„Äā
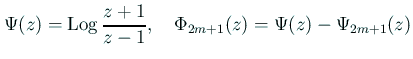
„Ā®„Āó„Ā¶„ÄĀ
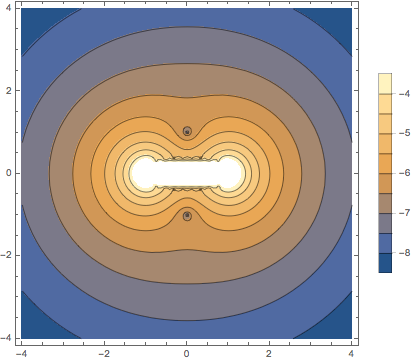
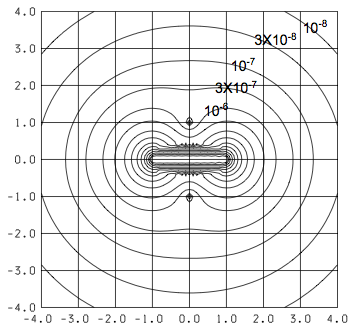
(„Āď„āĆ„ĀĮś£ģ [12] „Āę„Āā„āčŚõ≥„Ā®Ť¶čśĮĒ„ĀĻ„āč„Āü„āĀ„Āß„Āā„āč„Äā)
 |
|
„Éó„É≠„āį„É©„Ɇ„ĀĮ„ÄĀ
šĽėťĆ≤ ![[*]](crossref.gif) „ā퍶č„āą„Äā
„ā퍶č„āą„Äā
![]() ŚĻ≥ťĚĘ„Āę„Āä„ĀĄ„Ā¶„ÄĀÁ©ćŚąÜŚĆļťĖď
ŚĻ≥ťĚĘ„Āę„Āä„ĀĄ„Ā¶„ÄĀÁ©ćŚąÜŚĆļťĖď ![]() „Āč„āČťĀ†„ĀĖ„Āč„āč„Ā®„ÄĀ
„Āč„āČťĀ†„ĀĖ„Āč„āč„Ā®„ÄĀ
![]() „ĀƜĕťÄü„ĀęśłõŚįĎ„Āô„āč„Āď„Ā®„ĀĆŚąÜ„Āč„āč„Äā
„Āď„Āģ„āą„ĀÜ„Ā™śĆôŚčē„ĀĆŚ§ö„ĀŹ„ĀģśēįŚÄ§Á©ćŚąÜŚÖ¨ŚľŹ„ĀęŚÖĪťÄö„Āó„Ā¶Ť¶č„āČ„āĆ„āč„Āď„Ā®„ĀĮ„ÄĀ
„ĀƜĕťÄü„ĀęśłõŚįĎ„Āô„āč„Āď„Ā®„ĀĆŚąÜ„Āč„āč„Äā
„Āď„Āģ„āą„ĀÜ„Ā™śĆôŚčē„ĀĆŚ§ö„ĀŹ„ĀģśēįŚÄ§Á©ćŚąÜŚÖ¨ŚľŹ„ĀęŚÖĪťÄö„Āó„Ā¶Ť¶č„āČ„āĆ„āč„Āď„Ā®„ĀĮ„ÄĀ
![[*]](crossref.gif) „ĀߍŅį„ĀĻ„Āü„Āď„Ā®„Āč„āČÁźÜŤß£„Āß„Āć„āč„Äā
„ĀߍŅį„ĀĻ„Āü„Āď„Ā®„Āč„āČÁźÜŤß£„Āß„Āć„āč„Äā
„Āď„ĀģŚõ≥„ĀĮŚģüťöõÁöĄ„Ā™Ť™§Ś∑ģŤ©ēšĺ°„ĀęšĹŅ„ĀÜ„Āď„Ā®„ĀĆŚáļśĚ•„āč„Äā
„āā„ĀÜ1„Ā§„ÄĀśúČťôźŚĆļťĖďšłä„ĀģśēįŚÄ§Á©ćŚąÜŚÖ¨ŚľŹ„ĀģŤ™§Ś∑ģ„ĀģÁČĻśÄßťĖĘśēį„Āģšĺč„āí„Āā„Āí„Ā¶„Āä„ĀŹ„Äā „Āď„ĀģŤ¨õÁĺ©„Āß„ĀĮŤß£Ť™¨„Āó„Ā¶„ĀĄ„Ā™„ĀĄ„ĀĆ„ÄĀ śúČŚźć„Ā™ Gauss-Legendre ŚÖ¨ŚľŹ„ĀģŚ†īŚźą„āíÁīĻšĽč„Āô„āč„Äā
![]() ś¨°„Āģ Gauss-Legendre ŚÖ¨ŚľŹ„ĀĮ„ÄĀ
ś¨°„Āģ Gauss-Legendre ŚÖ¨ŚľŹ„ĀĮ„ÄĀ
![]() ś¨°„ĀģÁõīšļ§Ś§öť†ÖŚľŹ„Āģ
ś¨°„ĀģÁõīšļ§Ś§öť†ÖŚľŹ„Āģ![]() ŚÄč„Āģťõ∂ÁāĻ„āíś®ôśú¨ÁāĻ„ĀęšĹŅ„ĀĄ„ÄĀ
ŚÄč„Āģťõ∂ÁāĻ„āíś®ôśú¨ÁāĻ„ĀęšĹŅ„ĀĄ„ÄĀ
![]() ś¨°„Āĺ„Āß„ĀģŚ§öť†ÖŚľŹ„Āę„Ā§„ĀĄ„Ā¶ś≠£ÁĘļ„Ā™Á©ćŚąÜ„ā퍮ąÁģó„Āß„Āć„āč„Äā
„Ā§„Āĺ„āä15šĹć„ĀģŚÖ¨ŚľŹ„Āß„Āā„āč„Äā
Śģüťöõ
ś¨°„Āĺ„Āß„ĀģŚ§öť†ÖŚľŹ„Āę„Ā§„ĀĄ„Ā¶ś≠£ÁĘļ„Ā™Á©ćŚąÜ„ā퍮ąÁģó„Āß„Āć„āč„Äā
„Ā§„Āĺ„āä15šĹć„ĀģŚÖ¨ŚľŹ„Āß„Āā„āč„Äā
Śģüťöõ
![]() „Āģśõ≤Á∑ö„ĀĆŤ¶č„Āą„ÄĀ
„Āģśõ≤Á∑ö„ĀĆŤ¶č„Āą„ÄĀ
![]() ÁāĻ Simpson ŚÖ¨ŚľŹ„āą„āä„āāś†ľśģĶ„Āꍙ§Ś∑ģ„ĀģÁČĻśÄßťĖĘśēį„ĀģŚÄ§„ĀĆŚįŹ„Āē„ĀĄ
(
ÁāĻ Simpson ŚÖ¨ŚľŹ„āą„āä„āāś†ľśģĶ„Āꍙ§Ś∑ģ„ĀģÁČĻśÄßťĖĘśēį„ĀģŚÄ§„ĀĆŚįŹ„Āē„ĀĄ
(![]() ś°Āšłč„ÄĀ„Ā§„Āĺ„āä1ŚĄĄŚąÜ„Āģ1) „Āď„Ā®„ĀĆŚąÜ„Āč„āč„Äā
ś°Āšłč„ÄĀ„Ā§„Āĺ„āä1ŚĄĄŚąÜ„Āģ1) „Āď„Ā®„ĀĆŚąÜ„Āč„āč„Äā
ś°āÁĒį Á•źŚŹ≤