Next: 5.5 台形公式の誤差解析 Up: 5 数値積分の高橋・森による誤差解析理論 Previous: 5.3 誤差の特性関数の例 (1) 有限区間の場合の古典的公式
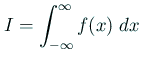
に対する台形公式
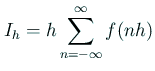
の場合、
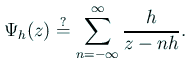
実はこれは残念ながら収束しない。しかし次のように小修正すれば良い。
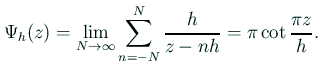
一方、
![]() はどうすべきか?
有限の
はどうすべきか?
有限の ![]() の場合の
の場合の
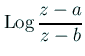 の適当な極限として
の適当な極限として
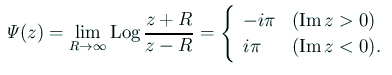
(最後の等式の証明も手頃な問題かな?と思ったので残す。 余談
![[*]](crossref.gif) と見比べると良い。)
実際にこの
と見比べると良い。)
実際にこの
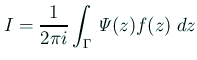
が成り立つことは直接簡単に証明できる。
これから
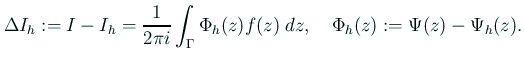
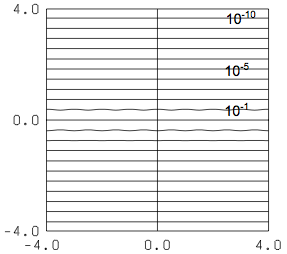
![]() の等高線を見よう。
の等高線を見よう。
ぞっとするほど小さいことが見て取れる。
 |
桂田 祐史