Next: 3.2 での減衰の速い解析関数の積分 に対する台形公式 Up: 3.1 滑らかな周期関数の1周期の積分 Previous: 3.1.1 数値例
周期関数の一周期積分が台形公式でうまく計算できることは、 次の定理を用いることでひとまず説明できる。

|
Euler や MacLaurin は、
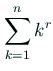 (
(
![]() )
や
)
や
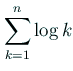 を評価するためにこの公式を導出したが、
この文書の立場では、台形公式の誤差を表す公式と見ることが出来る。
を評価するためにこの公式を導出したが、
この文書の立場では、台形公式の誤差を表す公式と見ることが出来る。
![]() が
が ![]() の周期であれば、
の周期であれば、![]() が 0
になり、
が 0
になり、
であることが期待される。
もっとも、具体的な問題に対して、この公式で誤差がどの程度になるかを 調べるのは難しい。
桂田 祐史