3.1.1 数値例

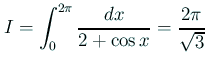$I=\dsp\int_{0}^{2\pi}\frac{\Dx}{2+\cos x}=\frac{2\pi}{\sqrt{3}}$ . もう少し複雑なものが欲しければ、 Bessel関数の積分表示¹、 振り子の周期の計算など。

$ cat example4.c
$ cc -o example4 example4.c
$ ./example4 > ex4.data
$ cat ex4.data
#   N       I-M_N           I-T_N         I-S_N
    2    4.860061e-01  -5.611915e-01  -1.259323e+00
    4    3.720712e-02  -3.759270e-02   1.369402e-01
    8    1.927779e-04  -1.927882e-04   1.227385e-02
   16    5.122576e-09  -5.122576e-09   6.425590e-05
   32    8.881784e-16   4.440892e-16   1.707525e-09
   64    4.440892e-16  -1.776357e-15   8.881784e-16
  128   -1.776357e-15  -4.440892e-16  -4.440892e-16
  (以下略)
$ gnuplot example4.gp -

図: $I=\dsp\int_0^{2\pi}\frac{1}{2+\cos x}\;dx$ を中点公式, 台形公式, Simpson公式で計算したときの誤差

$N=32$ の段階で、台形公式の誤差 $\vert I-T_N\vert\simeq 4.4\times 10^{-16}$ . ほぼ使用している処理系の最高精度に到達している ²。 $\qedsymbol$

前節の例を知った後では、 この例の結果が異常に思えるくらい良いことが分かるであろう。

事実4

(実は)滑らかな周期関数の1周期の積分を台形公式で計算すると、 小さい $N$ でも高精度な値が得られる。