Next: 参考文献 Up: 4 Laplace 方程式の境界値問題を数値計算で解く Previous: 4.3 有限要素法, FreeFem++
速度ポテンシャルを求める境界値問題
特に
![]() ,
,
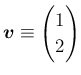 のときは、
のときは、
![]() において
において
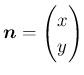 であるから、
であるから、
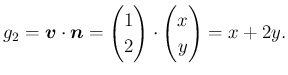
| 速度ポテンシャルを求める potential2d.edp |
// potential2d.edp
// 2次元非圧縮ポテンシャル流
// 速度ポテンシャル、流れ関数、速度を求め
// 等ポテンシャル線, 流線, 速度場を描く
border Gamma(t=0,2*pi) { x = cos(t); y = sin(t); } // 円盤領域
int m=40;
mesh Th=buildmesh(Gamma(m));
plot(Th, wait=1, ps="Th.eps");
fespace Vh(Th,P1);
Vh u, v, phi, psi;
func Vn=x+2*y; // Ωが単位円で, V=(1,2) のとき V・n=x+2y
// 速度ポテンシャルφを求め、その等高線 (等ポテンシャル線) を描く
solve Laplace(phi,v) =
int2d(Th)(dx(phi)*dx(v)+dy(phi)*dy(v))
-int1d(Th,Gamma)(Vn*v);
plot(phi,ps="contourpotential.eps",wait=1);
// 流れ関数ψを求め、その等高線 (流線) を描く (ちょっと安直なやり方)
func Vn2=y-2*x;
solve Laplace2(psi,v) =
int2d(Th)(dx(psi)*dx(v)+dy(psi)*dy(v))
-int1d(Th,Gamma)(Vn2*v);
plot(psi,ps="streamline.eps",wait=1);
// 等ポテンシャル線と流線を同時に描く
// plot(phi,psi,ps="lines.esp", wait=1);
// ベクトル場 (u,v)=∇φ を描く (ちょっと雑なやり方)
u=dx(phi);
v=dy(phi);
plot([u,v],ps="vectorfield.eps");
|
プログラムはテキスト・エディター (テキスト・エディット, mi, emacs など) で作成し、ターミナルから、
| こんなふうにして実行 |
FreeFem++ solveLapalce.edp |
(実は、上の弱形式は解の一意性がないので、 このプログラムは少し危ういところがある。)
桂田 祐史