| (再1) | ||
| (再2) | 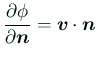 (on (on |
速度ポテンシャルを求める境界値問題
特に
![]() ,
,
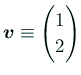 のときは、
のときは、
![]() において
において
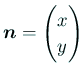 であるから、
であるから、
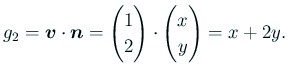
| 速度ポテンシャルを求める solveLaplace.edp |
// solveLaplace.edp
border Gamma2(t=0,2*pi) { x=cos(t); y=sin(t); }
int m=40;
mesh Th = buildmesh(Gamma2(m));
plot(Th, wait=1, ps="Th.eps");
savemesh(Th,"Th.msh"); // optional
fespace Vh(Th,P1);
Vh u,v;
func f=0;
func g1=0; // no use
func g2=x+2*y;
solve Poisson(u,v) =
int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
-int2d(Th)(f*v)
-int1d(Th,Gamma2)(g2*v) // +on(Gamma1,u=g1)
;
plot(u,ps="equipotential.eps");
|
プログラムはテキスト・エディター (テキスト・エディット, mi, emacs など) で作成し、ターミナルから、
| こんなふうにして実行 |
| FreeFem++ solveLapalce.edp |
(実は、上の弱形式は解の一意性がないので、 このプログラムは少し危ういところがある。)