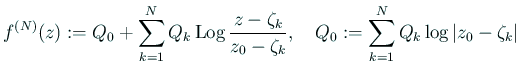

Next: 4.6 Eigen ライブラリィを用いた計算プログラム
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4.4 (1), (2) を解くための
4.5 (3), (4) を基本解の方法で解く
(この項は書きかけです。)
写像関数
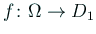 を求めるための、境界値問題
を求めるための、境界値問題
を基本解の方法 (FSM) で解いてみよう。
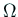 の外部に
の外部に 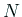 個の点
個の点 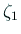 ,
, 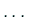 ,
, 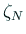 を取り、
を取り、
とおく。ここで 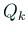 (
(
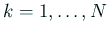 ) は未知の実定数である。
一方、
) は未知の実定数である。
一方、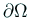 から
から 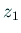 ,
, 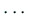 ,
, 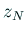 を選び、
を選び、
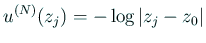
(
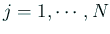
)
で 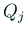 を定める。具体的には連立1次方程式
を定める。具体的には連立1次方程式
を解けばよい。
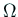 を
を 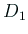 に写す等角写像を求めてみよう。
実部が
に写す等角写像を求めてみよう。
実部が 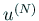 と一致する正則関数
と一致する正則関数 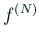 が求まれば、
が求まれば、
が等角写像の近似になることが期待できる。
簡単のため、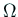 は
は 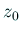 に関して星型であるとする。
このとき
に関して星型であるとする。
このとき
は実部が 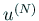 に等しい正則関数である。
に等しい正則関数である。
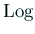 を使っているが、
を使っているが、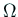 全体で一価正則な関数になっている。
全体で一価正則な関数になっている。


Next: 4.6 Eigen ライブラリィを用いた計算プログラム
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4.4 (1), (2) を解くための
桂田 祐史
2015-07-22
![]() を求めるための、境界値問題
を求めるための、境界値問題
![]() の外部に
の外部に ![]() 個の点
個の点 ![]() ,
, ![]() ,
, ![]() を取り、
を取り、
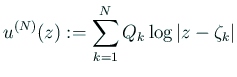
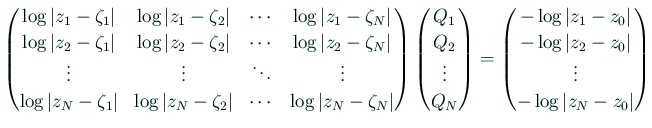
![]() を
を ![]() に写す等角写像を求めてみよう。
実部が
に写す等角写像を求めてみよう。
実部が ![]() と一致する正則関数
と一致する正則関数 ![]() が求まれば、
が求まれば、
![]() は
は ![]() に関して星型であるとする。
このとき
に関して星型であるとする。
このとき