

Next: 4.2 FreeFem++ とは
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4 Laplace 方程式の境界値問題を数値計算で解く
1つは速度ポテンシャルに対する Neumann 境界値問題で、
というもの。この場合は、
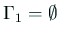 ,
,
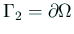 ,
, 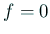 ,
,
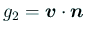 とすれば良い。
とすれば良い。
もう1つは、
領域 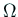 の写像関数
の写像関数
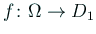 を求めるための Dirichlet 境界値問題で、
を求めるための Dirichlet 境界値問題で、
ただし 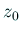 は
は 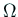 から選んだ任意の1点である。
この
から選んだ任意の1点である。
この 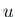 の1つの共役調和関数を
の1つの共役調和関数を 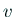 として、
として、
で 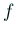 が得られる。
が得られる。


Next: 4.2 FreeFem++ とは
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4 Laplace 方程式の境界値問題を数値計算で解く
桂田 祐史
2015-07-22
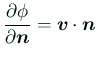 (on
(on ![]() の写像関数
の写像関数
![]() を求めるための Dirichlet 境界値問題で、
を求めるための Dirichlet 境界値問題で、