

Next: 4.4 (1), (2) を解くための
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4.2 FreeFem++ とは
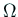 を
を
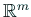 の有界な領域、
その境界
の有界な領域、
その境界 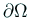 が
が 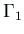 ,
, 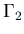 に分かれているとする。
に分かれているとする。
このとき、Poisson 方程式の境界値問題
|
(5) |
|
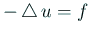 (in (in 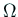 )
) |
|
(6) |
|
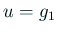 (on (on 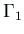 )
) |
|
(7) |
|
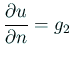 (on (on 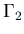 )
) |
は、次のように弱定式化される。
Find
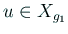 s.t.
s.t.
ここで
それから念のため:
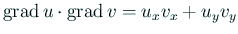 .
.


Next: 4.4 (1), (2) を解くための
Up: 4 Laplace 方程式の境界値問題を数値計算で解く
Previous: 4.2 FreeFem++ とは
桂田 祐史
2015-07-22
![]() を
を
![]() の有界な領域、
その境界
の有界な領域、
その境界 ![]() が
が ![]() ,
, ![]() に分かれているとする。
に分かれているとする。
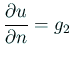 (on
(on ![]() s.t.
s.t.
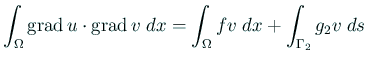 (
(