Next: E..1.3 жђБуХџсЂІсЂцLipschitzТЮАС╗ХсѓњТ║ђсЂЪсЂЎта┤тљѕсЂ«УДБсЂ«тГўтюесЂеСИђТёЈТђД Up: E..1 LipschitzТЮАС╗ХсѓњС╗«т«џсЂЎсѓІта┤тљѕ Previous: E..1.1 BanachуЕ║жќЊ
т«їтѓЎУиЮжЏбуЕ║жќЊсЂФсЂцсЂёсЂдсЂ» Banach сЂ«СИЇтІЋуѓ╣т«џуљєсЂесЂёсЂєжЄЇУдЂсЂфт«џуљєсЂїсЂѓсѓІсђѓ
![]() сѓњУиЮжЏбуЕ║жќЊсЂесЂЎсѓІсђѓ
сѓњУиЮжЏбуЕ║жќЊсЂесЂЎсѓІсђѓ
тєЎтЃЈ
![]() сЂФсЂцсЂёсЂдсђЂ
сЂФсЂцсЂёсЂдсђЂ
![]() сЂї
сЂї ![]() сЂ«СИЇтІЋуѓ╣сЂДсЂѓсѓІсЂесЂ»сђЂ
сЂ«СИЇтІЋуѓ╣сЂДсЂѓсѓІсЂесЂ»сђЂ
тєЎтЃЈ
![]() сЂїуИ«т░ЈтєЎтЃЈсЂДсЂѓсѓІсЂесЂ»сђЂ
сЂїуИ«т░ЈтєЎтЃЈсЂДсЂѓсѓІсЂесЂ»сђЂ

|
Step 1
С╗╗ТёЈсЂ«
![]() сЂФт»ЙсЂЌсЂд
сЂФт»ЙсЂЌсЂд
Step 2
![]() сЂ»
сЂ» ![]() сЂФсЂісЂЉсѓІ Cauchy тѕЌсЂДсЂѓсѓІсђѓ
т«ЪжџЏсђЂ
сЂФсЂісЂЉсѓІ Cauchy тѕЌсЂДсЂѓсѓІсђѓ
т«ЪжџЏсђЂ
![]() ,
, ![]() сЂесЂЎсѓІсЂесЂЇ
сЂесЂЎсѓІсЂесЂЇ
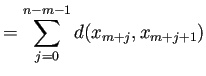 |
||
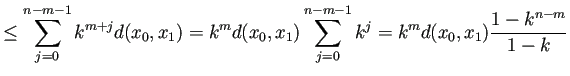 |
||
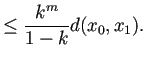 |
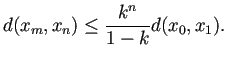
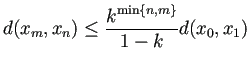
Step 3
![]() сЂ»т«їтѓЎсЂДсЂѓсѓІсЂІсѓЅсђЂ сЂѓсѓІ
сЂ»т«їтѓЎсЂДсЂѓсѓІсЂІсѓЅсђЂ сЂѓсѓІ
![]() сЂїтГўтюесЂЌсЂдсђЂ
сЂїтГўтюесЂЌсЂдсђЂ
сЂЋсЂдсђЂ
![]() ,
,
![]() сЂФт»ЙсЂЌсЂдсђЂ
сЂФт»ЙсЂЌсЂдсђЂ
![]() сѓњС╗ЦСИІсЂ«сѓѕсЂєсЂФтИ░у┤ЇуџёсЂФт«џсѓЂсѓІсђѓ
сѓњС╗ЦСИІсЂ«сѓѕсЂєсЂФтИ░у┤ЇуџёсЂФт«џсѓЂсѓІсђѓ
уИ«т░ЈтєЎтЃЈсЂ«т«џуљєсЂ«у│╗сЂесЂЌсЂдтЙЌсѓЅсѓїсѓІТгАсЂ«т«џуљєсЂ»жЮътИИсЂФтй╣уФІсЂцсђѓ
![\begin{jtheorem}[тєфсЂїуИ«т░ЈтєЎтЃЈсЂфсѓЅсЂ░СИЇтІЋуѓ╣сѓњТїЂсЂц]
$X$\ сѓњ $\math...
...сЂЇ $\left\{x_n\right\}$\ сЂ» $T$\ сЂ«СИЇтІЋуѓ╣сЂФтЈјТЮЪсЂЎсѓІсђѓ
\end{jtheorem}](img799.png)
|
С╗╗ТёЈсЂ« ![]() сѓњтЈќсЂБсЂдсђЂ
сѓњтЈќсЂБсЂдсђЂ
ТАѓућ░ уЦљтЈ▓