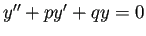 (
(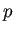 ,
, 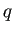 は定数) の
一般解は次のように求まる。
は定数) の
一般解は次のように求まる。
- (i)
-
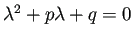 が相異なる
が相異なる 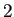 根
根 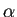 ,
, 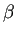 を持
つならば、
を持
つならば、
- (ii)
-
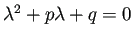 が重根
が重根 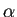 を持つならば、
を持つならば、
- (iii)
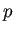 ,
, 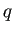 が実定数で、
が実定数で、
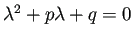 が虚根
が虚根 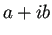 (
(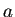 ,
,
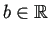 ;
; 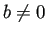 ) を持つならば、
) を持つならば、
このように 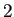 階方程式の一般解は、
適当な二つの関数
階方程式の一般解は、
適当な二つの関数 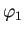 ,
, 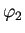 を用いて、
を用いて、
と書ける場合がしばしばあるが、
このとき 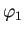 ,
, 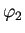 を
基本解 (fundamental solution) とよぶ。
つまり
を
基本解 (fundamental solution) とよぶ。
つまり
- 特性方程式が相異なる
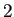 根
根 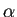 ,
, 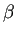 を持つ場合、
を持つ場合、
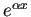 ,
,
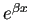 は基本解
は基本解
- 特性方程式が相異なる重根
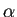 を持つ場合、
を持つ場合、
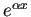 ,
,
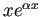 は基本解
は基本解
- 特性方程式が互いに複素共役である
虚根
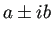 を持つ場合、
を持つ場合、
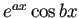 ,
,
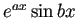 は基本解
は基本解
桂田 祐史
![]() 階方程式の一般解は、
適当な二つの関数
階方程式の一般解は、
適当な二つの関数 ![]() ,
, ![]() を用いて、
を用いて、