Next: B..2.1.1 odeint() の利用 Up: B..2 Python によるシミュレーション Previous: B..2 Python によるシミュレーション
Malthus モデルの初期値問題
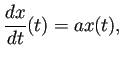 |
(B.2) | |
| (B.3) |
scipy の odeint(func, y0, t [,args,Dfun,col_deriv,
![]() ]]) という関数を使って初期値問題
]]) という関数を使って初期値問題
![\begin{subequations}% 2023-09-25 00:39の式群
\begin{align}&\frac{\D y}{\D t}=f(y,t)\quad\text{($t\in[t_0,T]$)}\\ &y(t_0)=y_0 \end{align}\end{subequations}](img493.png) |
念のため: ODE は ordinary differential equation (常微分方程式) の頭文字を取って作った略称である。