Next: 2.2 一般解 Up: 2 マルサスMalthus の法則 Previous: 2 マルサスMalthus の法則
実変数 ![]() についての未知関数
についての未知関数 ![]() について
について
この方程式は次のようにも書かれる。
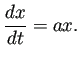 |
(2.2) |
![]() の場合として、
人口論の マルサスMalthus の法則のモデルがある。
の場合として、
人口論の マルサスMalthus の法則のモデルがある。
![]() の場合として、放射性元素の崩壊のモデルがある。
の場合として、放射性元素の崩壊のモデルがある。
用語の確認をしておこう。
方程式 (F.2) は、1階正規形の微分方程式 (normal form of first order differential equation) である。
一般に、適当な関数 ![]() を用いて
を用いて
| (2.3) |
問
(F.2) の場合に ![]() は何か。
は何か。