

Next: 3.3 前進 Euler 法の収束証明
Up: 3 基本的な概念・用語
Previous: 3.1.0.1 問
解法 (3) の、
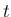 における局所離散化誤差 (local truncation error) を
における局所離散化誤差 (local truncation error) を
で、また大域的離散化誤差 (global
discretization error, global truncation error) を
で定義する。
これを用いて公式の次数 (order, 位数とも呼ぶ) を
次のように定義する。
あらく言って 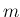 次の公式とは、
Taylor 展開して考えたとき、
次の公式とは、
Taylor 展開して考えたとき、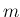 次の項まで一致するものであって、
次のような性質を持つ:
次の項まで一致するものであって、
次のような性質を持つ:
- (i)
- (どういうわけか運良く) 第
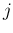 ステップまで誤差なく計算出来たとすると
ステップまで誤差なく計算出来たとすると
- (ii)
- 実際は誤差が累積するので
この左辺を全離散化誤差 (total discretization
error) と呼ぶ。
| 収束のための条件 |
以下の三条件が成り立つならば、
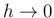 とするとき、近似解が真の解に収束することが証明できる。
とするとき、近似解が真の解に収束することが証明できる。
- (i)
- 公式の次数が少なくとも
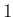 以上
(適合条件 (consistency) を満たす)。
以上
(適合条件 (consistency) を満たす)。
- (ii)
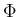 が
が
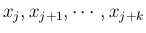 について Lipschitz 条件を満たす。
について Lipschitz 条件を満たす。
- (iii)
- 初期値
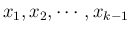 が適切に用意される。
が適切に用意される。
|


Next: 3.3 前進 Euler 法の収束証明
Up: 3 基本的な概念・用語
Previous: 3.1.0.1 問
桂田 祐史
2015-05-30
![$\displaystyle \tau(t,h):=\frac{1}{h}
\left[
x(t+k h)-L(t,t+h,\cdots,t+k h,x(t),x(t+h),\cdots,x(t+k h))
\right]
$](img72.gif)
![$\displaystyle \tau(t,h):=\frac{1}{h}
\left[
x(t+k h)-L(t,t+h,\cdots,t+k h,x(t),x(t+h),\cdots,x(t+k h))
\right]
$](img72.gif)
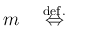
![]() 次の公式とは、
Taylor 展開して考えたとき、
次の公式とは、
Taylor 展開して考えたとき、![]() 次の項まで一致するものであって、
次のような性質を持つ:
次の項まで一致するものであって、
次のような性質を持つ: