もっとも簡単な前進 Euler 法の場合に近似解が厳密解に収束することを 証明してみよう。
|
|
![]() が
が ![]() 級であるから、
級であるから、![]()
![]() s.t.
s.t.
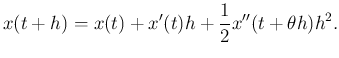
![]() であることに注意して、
であることに注意して、![]() ,
,
![]() とおくと、
とおくと、
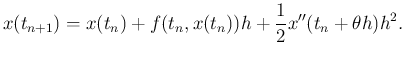
Euler 法の公式より
であるから、辺々引き算して
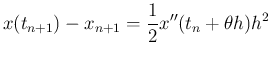
を得る。 これから Euler 法の局所離散化誤差は
さて、![]() が
が ![]() 級であることから
級であることから
が存在する。
(4) から
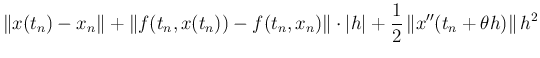 | |||
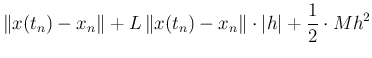 | |||
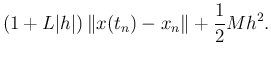 |
とおくと、
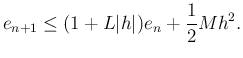
![$\displaystyle \frac{(1+L\vert h\vert)^n-1}{L\vert h\vert}\cdot \frac{1}{2} M h^2
=\frac{M\vert h\vert}{2L}\left[(1+L\vert h\vert)^n-1\right]$](img113.gif) | |||
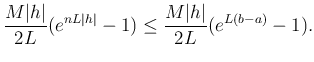 |
|
|
(なんか、Gronwall の数列版か?)
|
|
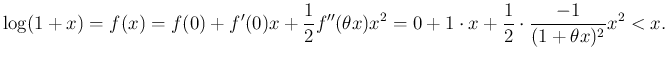
ゆえに
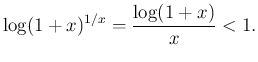
これから