Next: 2.2.3 еҫ©зҝ’: ж №гҒЁдҝӮж•°гҒ®й–ўдҝӮ Up: 2.2 йҖЈз«Ӣжі•, зү№гҒ« Durand-Kerner Previous: 2.2.1 Durand-Kerner жі•
Durand гҒҜ (2.5) гҒ®еҸҺжқҹжҖ§гӮ’зӨәгҒ—гҖҒжңҖзөӮзҡ„гҒ« ![]() д№—еҸҺжқҹ
гҒ«гҒӘгӮӢгҒ“гҒЁгӮ’иЁјжҳҺгҒ—гҒҹгҖӮ
д№—еҸҺжқҹ
гҒ«гҒӘгӮӢгҒ“гҒЁгӮ’иЁјжҳҺгҒ—гҒҹгҖӮ ![]()
![]() ,
, ![]() ,
, ![]() гҒҢгҒҷгҒ№гҒҰзӣёз•°гҒӘгӮҠгҖҒ
гҒҢгҒҷгҒ№гҒҰзӣёз•°гҒӘгӮҠгҖҒ![]() гҒҢ
гҒҢ
![]() гҒ«еҚҒеҲҶиҝ‘гҒ„гҒЁгҒ—гҒҰгҖҒ
гҒ«еҚҒеҲҶиҝ‘гҒ„гҒЁгҒ—гҒҰгҖҒ
![]() гҒЁгҒҠгҒ‘гҒ°гҖҒ
гҒЁгҒҠгҒ‘гҒ°гҖҒ
![$\displaystyle \eps_i^{(k)}
\left[
1-\frac{\prod_{j\ne i}(x_i^{(k)}-\xi_j)}
{\prod_{j\ne i}(x_i^{(k)}-x_j^{(k)})}
\right]$](img219.gif) | |||
![$\displaystyle \eps_{i}^{(k)}
\left[
1-\prod_{j\ne i}
\left(
1+\frac{\eps_j^{(k)}}{x_i^{(k)}-x_{j}^{(k)}}
\right)
\right]$](img220.gif) |
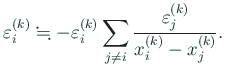
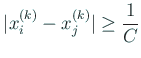
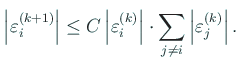
|
|
![\begin{jtheorem}
% latex2html id marker 573 [йҮҚеҝғгҒ®дёҚеӨүжҖ§]
д»»ж„ҸгҒ®еҲқжң...
...gin{displaymath}
\sum_{i=1}^n \eps_i^{(k+1)}=0.
\end{displaymath}\end{jtheorem}](img227.gif)
|
жЎӮз”° зҘҗеҸІ