ここでも 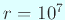 とする。
とする。
グレイゼル [9] によると、Napier は最初
の表を作ったそうだが、
公表した表は以下に説明するような三角関数の対数の表である。
Napier は真数として
を選んだ。
もちろん三角関数を用いた計算への応用が念頭であったためであろう。
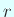 を
を 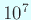 に選んだのは、
(ある程度大きくする必要があったこと以外に)
彼が利用できた最良の三角関数表の精度が
に選んだのは、
(ある程度大きくする必要があったこと以外に)
彼が利用できた最良の三角関数表の精度が 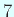 桁であったことによるらしい。
7桁精度の三角関数の値であるが、
桁であったことによるらしい。
7桁精度の三角関数の値であるが、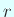 をかけることで値は整数になる。
実は Napier の時代には小数は普及していなかったため、
小数をさけるという目的があったらしい
(他ならない Napier が小数点記法の提唱者であることに注意)。
をかけることで値は整数になる。
実は Napier の時代には小数は普及していなかったため、
小数をさけるという目的があったらしい
(他ならない Napier が小数点記法の提唱者であることに注意)。
なお Napier の数表には、
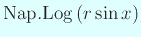 の値のうちの整数部分のみ提示されている
(小数点以下は切り捨てられている)。
の値のうちの整数部分のみ提示されている
(小数点以下は切り捨てられている)。
桂田 祐史
2019-03-01
![]() とする。
とする。
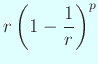
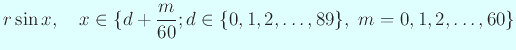
![]() の値のうちの整数部分のみ提示されている
(小数点以下は切り捨てられている)。
の値のうちの整数部分のみ提示されている
(小数点以下は切り捨てられている)。