Next: B..3 数表 (1) Up: B. Napier Previous: B..1 定義
隙間の小さな数表を得るには、![]() に近い数の冪を持ち出す必要があるので、
大きな
に近い数の冪を持ち出す必要があるので、
大きな ![]() に対して
に対して
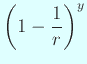
Napier の時代には小数の利用がまだ確立されていなかった。
そのために数表の多くは小数を避けるように作られるのが普通であったようだ。
例えば「三角関数表」も、
実際は大きな半径を持つ円の「正弦」を載せるのが普通であったらしく、
Napier が彼の対数表の「真数」として、
![]() (
(![]() は角度) を持ち出したのはもっともである。
彼が利用できる最良の三角関数表は 7 桁精度であったということは、
半径を
は角度) を持ち出したのはもっともである。
彼が利用できる最良の三角関数表は 7 桁精度であったということは、
半径を ![]() とした場合に小数点以下がなくなり整数になるということである。
とした場合に小数点以下がなくなり整数になるということである。
桂田 祐史