Next: 3 一般の場合の解析 Up: 2 惑星の運動方程式 Previous: 2.2 保存量
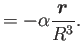
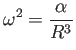
Why?
ところでエネルギー ![]() は
は
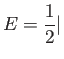
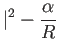
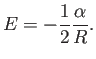
周期 ![]() は
は
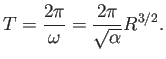
角運動量 (angular momentum) は、一般に、位置ベクトル ![]() と運動量
と運動量 ![]() のベクトル積として定義される:
のベクトル積として定義される:
初期時刻における角運動量を ![]() とする。
とする。
![]() の場合、..
衝突解と呼ばれる。
これは周期解にはならない。
この場合は、いわゆる Kepler の法則は
成り立たない。それに対して、
の場合、..
衝突解と呼ばれる。
これは周期解にはならない。
この場合は、いわゆる Kepler の法則は
成り立たない。それに対して、
![]() ならば Kepler の法則が成り立つ。
それを以下に見る。
ならば Kepler の法則が成り立つ。
それを以下に見る。