5.5 渦糸系

$N$ 個の渦糸からなる渦糸系の運動は、 $k$ 番目の渦糸の座標を $(x_k(t),y_k(t))$, 渦の強さを $\Gamma_k$ として、

$$\frac{\D x_k}{\D t}=\sum_{j=1\atop j\ne k}^N \frac{-\Gamma_j}{2\pi} \frac{y_k(t)-y_j(t)}{(x_k(t)-x_j(t))^2+(y_k(t)-y_j(t))^2}$$

$$\frac{\D y_k}{\D t}=\sum_{j=1\atop j\ne k}^N \frac{\Gamma_j}{2\pi} \frac{x_k(t)-x_j(t)}{(x_k(t)-x_j(t))^2+(y_k(t)-y_j(t))^2}$$

という微分方程式で表わされる。これは Hamilton 力学系であり、 数学的にはきれいな方程式であると言える。

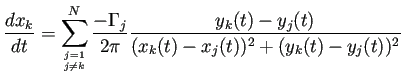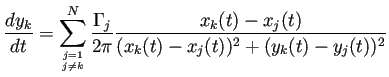参考書としては、岡本 [26]、 今井 [22] 第6章 (§44) 、 また中木 [23] も見ると良い。

稲垣亜希子・栗田智昭・田中賢史 [24] という卒業研究レポートがある。

(ひとり言) 竜巻とか、台風の藤原効果とか、渦関係で面白そうな話題は色々あるが、 チャレンジするには適度に簡単化しないと困難だと思われる。 渦糸はかなり大胆な簡単化だけれど、それでも自明でない構造を持っているらしい。 渦糸のシミュレーションのアニメーションは、見ていてとても楽しい。