3.7.1 定数係数線形常微分方程式

実数の定数 $a$, $b$, $c$, $d$ に対して、

という連立微分方程式を考える。初期条件として

$$x(0)=x_0,\quad y(0)=y_0$$ (21)

の形のものを考える。 これを解くプログラムを作成し、 解軌道 (曲線 $(x(t),y(t))$) を描け。 複数の解軌道を同時に描いてみよ。

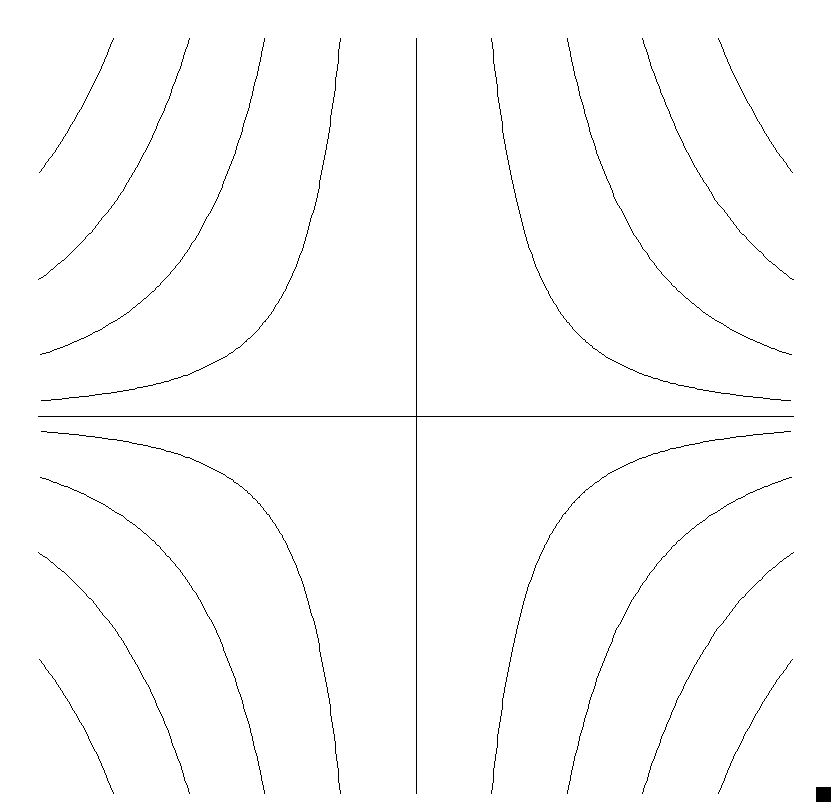
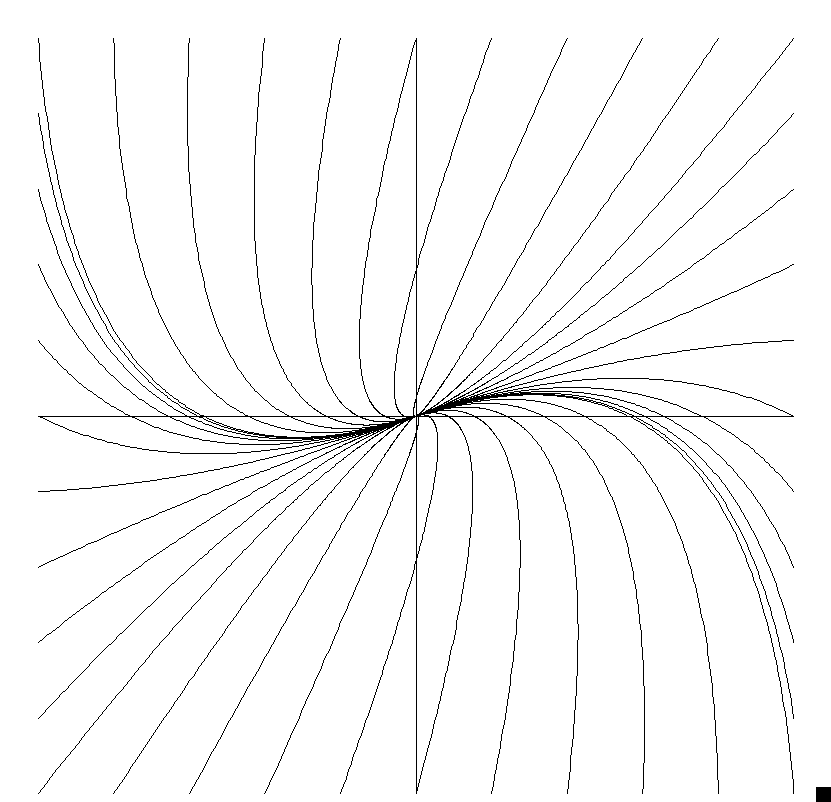
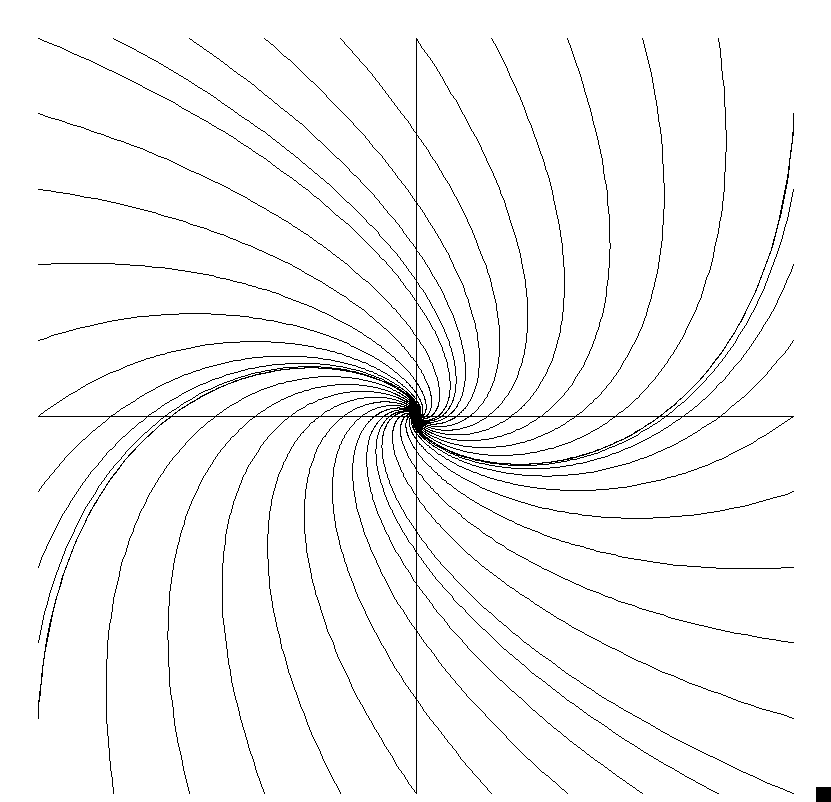
この微分方程式は、多くの現象の数理モデルとなる。 力学においては、 つりあいの位置の近くの微小振動を表す多くの微分方程式がこの形となる。 また、力学系の平衡点(不動点)の線形安定性解析の基礎となるので、 その観点からも重要である。

$$\bm{x}(t)=\begin{pmatrix}x(t) y(t)\end{pmatrix},\quad A=\begin... ...b c & d \end{pmatrix},\quad \bm{x}_0=\begin{pmatrix}x_0 y_0 \end{pmatrix}$$

とおくと、 (20a), (20b) は

$$\frac{\D\bm{x}}{\D t}(t)=A\bm{x}(t),$$ (22)

(21) は

$$\bm{x}(0)=\bm{x}_0$$ (23)

と表せる。 (22) の形の微分方程式は、 定数係数線形常微分方程式と呼ばれる。

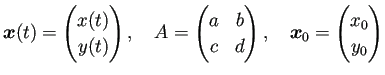
(22), (23) の解は、 行列の指数関数を用いると、次のように得られる。

$$\bm{x}(t)=e^{tA}\bm{x}_0.$$ (24)

これは基本的な問題であり、 微分方程式のテキストはもちろんであるが、 線形代数のテキストで言及されている場合もある。 笠原 [8] を推奨する (説明を端折る本が多い中で、親切な記述が嬉しい)。 あるいは、ちょっと雑であるけれど、 桂田 [2] (4節「定数係数線型常微分方程式」 特に§4.2.2) はアクセスしやすいかも。

図: $\ttmat{1}{0}{0}{-2}$

図: $\scriptsize \ttmat{-\frac{4}{5}}{-\frac{3}{5}} {\frac{2}{5}}{-\frac{11}{5}}$ (吸)

図: $\ttmat{\frac{8}{5}}{-\frac{9}{5}} {\frac{6}{5}}{-\frac{13}{5}}$ (湧)

図: $\ttmat{\frac{2}{5}}{\frac{9}{5}} {-\frac{1}{5}}{-\frac{8}{5}}$ (湧)

図: $\ttmat{-1}{2}{-1}{1}$

図: $\ttmat{0}{1}{-1}{-1}$