Next: Schwarz の不等式の別証明 Up: 2.5 線型部分空間への正射影 (1) Previous: 解答の分析
と書けるので、直交性の条件
から連立1次方程式
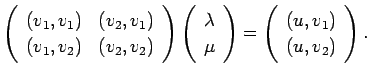
Schwarz の不等式の等号成立条件を吟味すると、 この連立1次方程式の係数行列は正則であることが分かるが 2.2、
![\begin{jdefinition}[線型部分空間への正射影]
$\R^n$\ の線型部分�...
...は \textbf{直交射影}
(orthogonal projection) と呼ぶ。
\end{jdefinition}](img18.gif)
|
実はより一般の部分集合 ![]() への正射影も定義できるが、それについては後述
する。
への正射影も定義できるが、それについては後述
する。
![\begin{jproposition}[正射影の特徴付け 「正射影は最も近い点」]...
...ert x-y\Vert=\dsp\min_{v\in V}\Vert x-v\Vert$.
\end{enumerate}\end{jproposition}](img19.gif)
|
ゆえに
これから
[(ii)
で定める。
であるから、
これが任意の
例題 1 の内容を命題としてまとめておこう。
![\begin{jproposition}[1次元部分空間への正射影]
$v\ne 0$\ とすると...
...aymath}
w=\frac{(u,v)}{(v,v)}v
\end{displaymath}である。
\end{jproposition}](img21.gif)
|
この ![]() 次元部分空間への正射影を用いると、
Schwarz の不等式の別証明を得る。
個人的には Schwarz の不等式の意味がよく分かる証明だと思っている。
次元部分空間への正射影を用いると、
Schwarz の不等式の別証明を得る。
個人的には Schwarz の不等式の意味がよく分かる証明だと思っている。
桂田 祐史