


Next: B..5 一般化された Strum 列
Up: B. Strum の方法
Previous: B..3.0.1 符号の変化数の計算に関する注意
(ここは単なる覚え書き。後で肉付けするかもしれない。)
![$ w\colon [a,b]\to\R$](img500.gif) は連続で、有限個の点で 0
になる他は正で、条件
は連続で、有限個の点で 0
になる他は正で、条件
を満たすような関数とする。このとき ![$ [a,b]$](img252.gif) 上の実数値連続関数全体の集合に
上の実数値連続関数全体の集合に
で定義される内積を導入して、内積空間としたものを 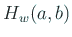 とする。
また
とする。
また
 に付随するノルムを
に付随するノルムを
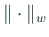 と書く:
と書く:
自然数 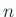 に対して、関数列
に対して、関数列
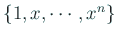 から Gram-Schimidt の
直交化法によって得られる直交多項式系を
から Gram-Schimidt の
直交化法によって得られる直交多項式系を
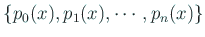 とする。
とする。



Next: B..5 一般化された Strum 列
Up: B. Strum の方法
Previous: B..3.0.1 符号の変化数の計算に関する注意
桂田 祐史
2015-12-22
![]() は連続で、有限個の点で 0
になる他は正で、条件
は連続で、有限個の点で 0
になる他は正で、条件
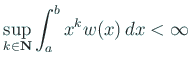
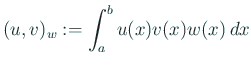
![]() に対して、関数列
に対して、関数列
![]() から Gram-Schimidt の
直交化法によって得られる直交多項式系を
から Gram-Schimidt の
直交化法によって得られる直交多項式系を
![]() とする。
とする。
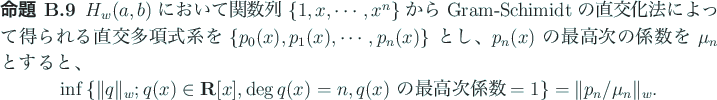
![\begin{jproposition}\upshape
$H_w(a,b)$\ において関数列 $\{1,x,\cdots,x^...
...はすべて単根で、区間 $[a,b]$\ の内部にある。
\end{jproposition}](img510.gif)

![\begin{jproposition}\upshape
$H_w(a,b)$\ において関数列 $\{1,x,\cdots,x^...
...aymath}は区間 $[a,b]$\ において Strum 列をなす。
\end{jproposition}](img512.gif)