3 三重対角化の手法

実対称行列に対する三重対角化の手法を学ぶ。

(1)

Givens 法

(2)

Householder 法

(3)

Lanczos 法

与えられた実対称行列 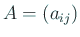$A=(a_{i j})$ に対し、適当な正則行列 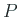$P$ を求め て

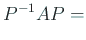
$$P^{-1} A P =$$   三重対角

とする。特に 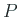$P$ として直交行列を取る。

歴史的には、Jacobi 法の変形として Givens 法が最初に現われたが、 その後現われた Householder 法は演算回数が約半分となるなど利点が多く、 普及している。大型疎行列に対しては Lanczos 法が有力な方法とされている。