


Next: 3.1.0.1 тЈѓУђЃ
Up: 3 СИЅжЄЇт»ЙУДњтїќсЂ«ТЅІТ│Ћ
Previous: 3 СИЅжЄЇт»ЙУДњтїќсЂ«ТЅІТ│Ћ
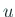 сѓњ
сѓњ 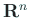 сЂ«тЇўСйЇсЃЎсѓ»сЃѕсЃФсЂесЂЎсѓІсђѓ
сЂ«тЇўСйЇсЃЎсѓ»сЃѕсЃФсЂесЂЎсѓІсђѓ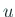 сЂФуЏ┤С║цсЂЎсѓІУХЁт╣│жЮб
сЂФуЏ┤С║цсЂЎсѓІУХЁт╣│жЮб
сЂФжќбсЂЎсѓІт»ЙуД░уД╗тІЋсѓњУАесЂЎтцЅТЈЏсѓњ 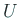 сЂесЂЎсѓІсЂесђЂ
сЂесЂЎсѓІсЂесђЂ
сЂДсЂѓсѓІсђѓ(
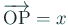 сЂфсѓІуѓ╣
сЂфсѓІуѓ╣ 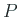 сЂІсѓЅ
сЂІсѓЅ 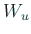 сЂФ
СИІсѓЇсЂЌсЂЪтъѓуиџсЂ«УХ│сѓњ
сЂФ
СИІсѓЇсЂЌсЂЪтъѓуиџсЂ«УХ│сѓњ
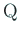 сЂесЂЎсѓІсЂесђЂ
сЂесЂЎсѓІсЂесђЂ
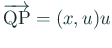 . сЂЮсѓїсѓєсЂѕсђЂ
. сЂЮсѓїсѓєсЂѕсђЂ
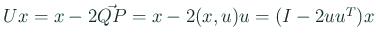 . сѓєсЂѕсЂФ
. сѓєсЂѕсЂФ 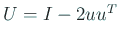 .)
.)
Subsections



Next: 3.1.0.1 тЈѓУђЃ
Up: 3 СИЅжЄЇт»ЙУДњтїќсЂ«ТЅІТ│Ћ
Previous: 3 СИЅжЄЇт»ЙУДњтїќсЂ«ТЅІТ│Ћ
ТАѓућ░ уЦљтЈ▓
2015-12-22
![]() сѓњ
сѓњ ![]() сЂ«тЇўСйЇсЃЎсѓ»сЃѕсЃФсЂесЂЎсѓІсђѓ
сЂ«тЇўСйЇсЃЎсѓ»сЃѕсЃФсЂесЂЎсѓІсђѓ![]() сЂФуЏ┤С║цсЂЎсѓІУХЁт╣│жЮб
сЂФуЏ┤С║цсЂЎсѓІУХЁт╣│жЮб
![\begin{jdefinition}[жЈАТўатцЅТЈЏсђЂHouseholder УАїтѕЌ]\upshape
$\R^n$\ сЂ«тЇўСй...
...Householder УАїтѕЌ} (сЂЙсЂЪсЂ»тЪ║ТюгуЏ┤С║цУАїтѕЌ) сЂетЉ╝сЂХсђѓ
\end{jdefinition}](img154.gif)
![\begin{jlemma}
% latex2html id marker 255 [жЈАТўатцЅТЈЏсЂ«ТђДУ│ф]\upshape
$U$\ ...
...ЏсЂДсЂѓсѓІсђѓ
\item $U$\ сЂ»т»ЙуД░тцЅТЈЏсЂДсЂѓсѓІсђѓ
\end{enumerate}\end{jlemma}](img155.gif)