1960 年代まで主流であった Jacobi 法について簡単に説明しよう。
これは実対称行列を ![]() 次元の回転変換により変形していって、対角成分以外
の成分の絶対値を小さくしていくというものであり、行列のサイズ
次元の回転変換により変形していって、対角成分以外
の成分の絶対値を小さくしていくというものであり、行列のサイズ ![]() が
が ![]() 程度の小さなものであれば現在でも実用的である。
程度の小さなものであれば現在でも実用的である。
なぜ「対角成分以外の成分の絶対値を小さくしていく」のか?これについて 説明しよう。まず次の定理は簡単であるが重要である。
|
|
![\begin{jtheorem}[Gerschgorin の円板定理 (1931)]\upshape
$A=(a_{i j})$\ に...
...�分をなせば、その中に $k$\ 個の
固有値がある。
\end{jtheorem}](img29.gif)
|
方程式
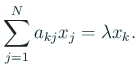
これから
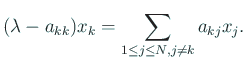
(以下
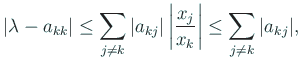
したがって
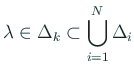 .
.
つぎに
とおくと、
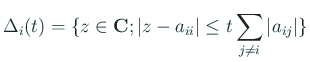
である。
![\begin{jcorollary}[狭義優対角行列は正則]\upshape
$N$\ 次正方行列...
...end{displaymath}が成り立てば、$A$\ は正則である。
\end{jcorollary}](img54.gif)
|
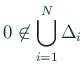 より、
0
は
より、
0
は なぜか今のカリキュラムの盲点となってしまって、 紹介されることがないが、 「代数方程式の根は方程式の係数の連続関数である」 行列の固有方程式の係数は、行列の成分の連続関数であることは明らかだから、 「行列の固有値は行列の成分の連続関数である」。 Gerschgorin の定理はあざやかに連続性を見せてくれる。