11.2 見掛けが少し異なる3つの Sylvester の慣性律

以下に現れる行列は (時々「実」を書き漏らすけれど) すべて実行列とする。

実対称行列 $A$ に対して、 $A$ の固有値のうちで正であるものの個数、 負であるものの個数、 0 であるものの個数をそれぞれ $\pi(A)$ , $\nu(A)$ , $\zeta(A)$ と書くことにする。

$A$ は $n$ 次正方行列として、

$$\pi(A),\nu(A),\zeta(A)\ge 0,\quad \pi(A)+\nu(A)+\zeta(A)=n$$

である。

まず実対称行列の実直交行列による対角化に関する常識的事項 (線形代数で習うはず) を復習する (これがなくても Sylvester の慣性律の証明は出来るわけだが、 使った方が私には見通しが良いので…)。

$A$ が$n$ 次実対称行列ならば、実直交行列 $U$ ( $U^{-1}=U^T$ ) と 実数 $\lambda_1$ , $\cdots$ , $\lambda_n$ が存在して、

$$U^T A U=\diag\left(\lambda_1,\cdots,\lambda_n\right).$$

ゆえに $\forall x\in\R^n$ に対して $y:=U^{-1} x$ とおくと、$x=U y$ で、

$$(Ax,x)=(A U y,U y)=(U^T A U y,y)=\sum_{j=1}^n \lambda_j y_j^2.$$

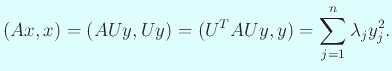
こうして2次形式 $(Ax,x)$ を平方和 -- 定数$\times ($何か$)^2$ の和 -- に変形できる。 平方完成と呼んでも良いだろうが、 これを2次形式の対角化という。 標語的に

平方完成は対角化である

と言っても良いであろう (筋の通った主張にするには色々言葉を足さなければいけないが、 迷子にならないために手短に言い切っておく)。

ところで、上の対角化の議論の要点は

(i)

$U^T A U$ が対角行列 $\diag\left(\lambda_1,\cdots,\lambda_n\right)$ である

(ii)

$U$ は正則

の二つである、と言えるだろう。

$(Ax,x)$ が平方和の形に書けるためには、 $U$ が実直交行列であることは必要ない (だから以下では $U$ でなく、 $P$ と書いたりする)。

$U$ が実直交行列でなければ、 $\lambda_j$ は $A$ の固有値とは限らないが、 $\lambda_j$ ( $j=1,\cdots,n$ ) のうちの正であるものの個数、 負であるものの個数は、$A$ で定まる。 それを定式化したものが、次の Sylvester の慣性律と呼ばれる定理である。

この定理は、 少し後で紹介する「良くテキストに載っている証明」からすると自然な主張であるが、 やや正体が分かりづらいのでは？と思う。 次の定理とセットにして覚えることを勧める。

証明. 定理 11.1 を認めた上での証明を与える。 $P$ として $U^T A U=\diag[\lambda_1,\cdots, \lambda_n]$ となるような実直交行列 $U$ を取れば、 $P^T A P=U^T AU=U^{-1} A U$ は $A$ の相似変換であり、 $\lambda_1$ , $\cdots$ , $\lambda_n$ は $A$ の固有値である。 ゆえに $n_p$ , $n_n$ , $n_z$ はそれぞれ $\pi(A)$ , $\nu(A)$ , $\zeta(A)$ に等しい。 $\qedsymbol$ $\qedsymbol$

杉原・室田 [8] には、 次の形の Sylvester の慣性律が載っている。

結論部分が「〜に依らず、〜で定まる」でなくて、 具体的な等式である点は、 定理 11.2 と同じである。 対角化でなくて、変換した行列 $B$ の固有値の話にしてしまうのも、 少なくとも彼らの目的 (固有値の数値計算アルゴリズムの議論をする) にとっては使いやすいようである。

ここでは、 定理11.2 と 定理11.3 が同等であること (一方を認めれば他方がすぐに導かれること) を見てみよう。

まず、定理11.3 を認めよう。 $n$ 次実対称行列 $A$ , 正則行列 $P$ に対して、 $\exists\lambda_1,\cdots,\lambda_n$ s.t. $P^T A P=\diag[\lambda_1,\cdots,\lambda_n]$ となったとすると、 $B:=P^T A P$ の固有値は (対角成分である) $\lambda_1$ , $\cdots$ , $\lambda_n$ であるから、

$$n_p=\pi(B)=\pi(A),\quad n_n=\nu(B)=\nu(A), \quad n_z=\zeta(B)=\zeta(A).$$

逆に定理 11.2 を認めよう。 実対称行列 $A$ , 正則行列 $P$ に対して、 $B:=P^T A P$ とおく。 $B$ は実対称行列であるから、適当な実直交行列 $U$ で対角化できる: $\exists\lambda_1,\cdots,\lambda_n\in\R$ s.t. $U^T B U=\diag[\lambda_1,\cdots,\lambda_n]$ . このとき

$$\diag\left(\lambda_1,\cdots,\lambda_n\right)=U^T B U=U^T P^T A P U =(PU)^T A (PU)=P'^T A P',$$

$$P':= PU.$$

$P$ と $U$ が正則であるから、$P'$ は正則である。 定理 11.2 から、 ($B$ の固有値である) $\lambda_1$ , $\cdots$ , $\lambda_n$ のうちで 正であるものの個数、負であるものの個数、0 であるものの個数は、 それぞれ $\pi(A)$ , $\nu(A)$ , $\zeta(A)$ に等しい。 ゆえに $\pi(B)=\pi(A)$ , $\nu(B)=\nu(A)$ , $\zeta(B)=\zeta(A)$ . $\qedsymbol$